CS1231S Tutorial 10 Solutions

This page has solutions for selected questions from this tutorial sheet.

This tutorial is on combinatorics, and basic probability. Please do not use these as lecture notes. You should make an earnest attempt and pretty much solve the tutorial questions before referring to the solutions. This means I will say “you should already know this/you should already know that” without much explanation on what exactly it is in detail.

Question 1

This is just another way of saying find the coefficient of the term $x^0$. The idea is to use the fact that:

$${\left(a+b\right)}^n=\sum _{i=0}^n\left(\genfrac{}{}{0ex}{}{n}{i}\right)a^i{b}^{n-i}$$

For ${\left(2x^2+\frac{1}{x}\right)}^9$, we can write it using the above identity to become:

$$\sum _{i=0}^9\left(\genfrac{}{}{0ex}{}{9}{i}\right)(2x^2{)}^i{x}^{-(9-i)}$$

Now, we need $2i+-(9-i)=0$, so $3i=9$ or $i=3$. Plugging that value of $i$ in, we get:

$$\left(\genfrac{}{}{0ex}{}{9}{3}\right)2^3=84\times 8=672$$

Question 2

So for this question we’re just picking a start point and an end point for the run of white balls.

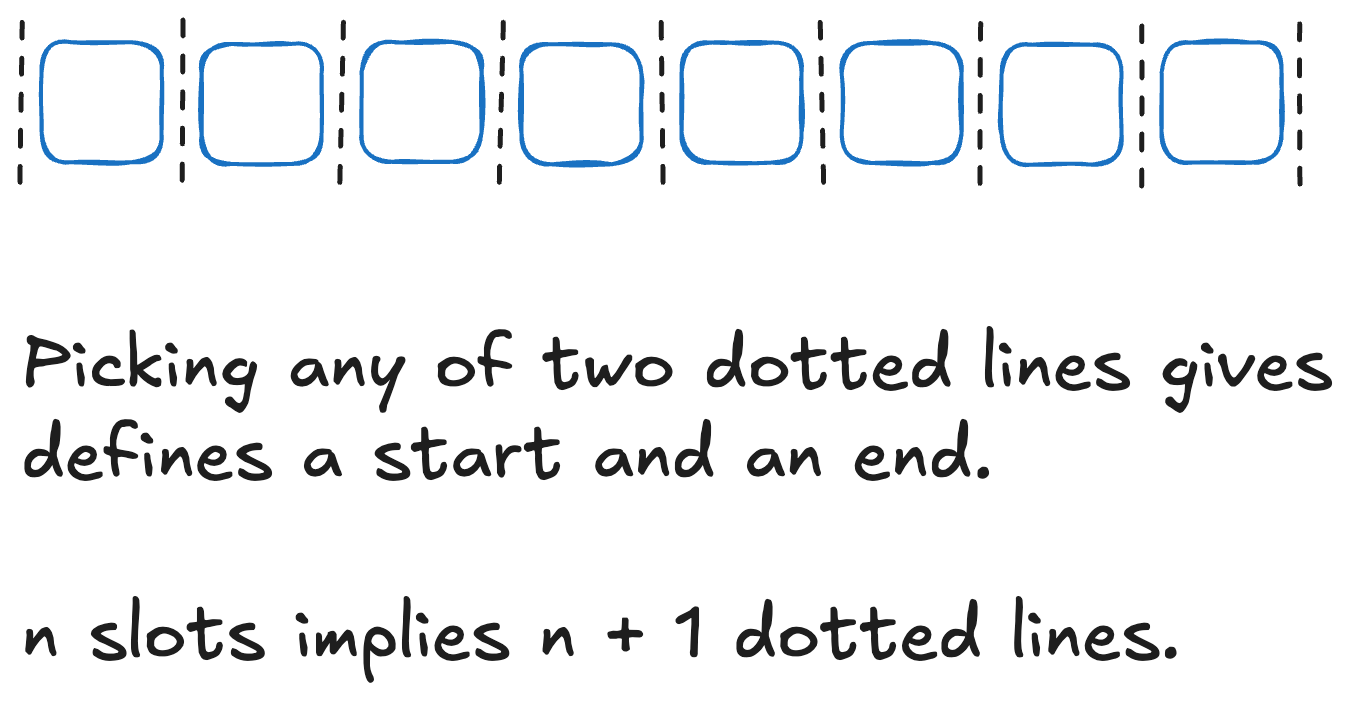
So from $n+1$ dotted lines, we wish to pick $2$ of them. $\left(\genfrac{}{}{0ex}{}{n+1}{2}\right)=\frac{(n+1)!}{2!\cdot (n-1)!}=\frac{(n+1)(n)}{2}$

Question 3

Part (a)

Let $p_i=Pr[D=i]$. Now we know that for $i\in \{1,2,3\}$ and $j\in \{4,5,6\}$, $p_i=2\cdot p_j$. You might be expected to infer from this that $p_1=p_2=p_3$ and $p_4=p_5=p_6$.

We also know that:

$$\begin{array}{rl}1& =p_1+p_2+p_3+p_4+p_5+p_6\\ & =3p_1+3p_4\\ & =3p_1+6p_1\\ & =9p_1\\ \frac{1}{9}& =p_1=p_2=p_3\\ \frac{2}{9}& =p_4=p_5=p_6\end{array}$$

Part (b)

So here’s the idea, we want $\mathbb{E}[X]$ where $X=\max (D_1,D_2)$ where $D_1$ and $D_2$ are random variables with the distribution from part (a), and $X$ is a random variable defined as above.

So first of all, we should probably try to find the distribution for $X$. To do this, it’s easier if we have the following probabilities for all $j\in \{1,2,4,5,6\}$:

$$Pr[D\le j]=\{\begin{array}{ll}0& ,j=0\\ \frac{1}{9}& ,j=1\\ \frac{2}{9}& ,j=2\\ \frac{3}{9}& ,j=3\\ \frac{5}{9}& ,j=4\\ \frac{7}{9}& ,j=5\\ \frac{9}{9}& ,j=6\end{array}$$

Now, the probability that $X=i$ is when exactly either $D_1=i$ and $D_2<i$ or $D_1<i$ and $D_2=i$, or $D_1=D_2=i$.

So working it out:

$$\mathrm{Pr}[X=1]=\mathrm{Pr}[D_1=1,D_2=1]=\mathrm{Pr}[D_1=1]\cdot \mathrm{Pr}[D_2=1]={\frac{1}{9}}^2$$ $$\begin{array}{rl}\mathrm{Pr}[X=2]& =\mathrm{Pr}[D_1=2,D_2\le 1]+\mathrm{Pr}[D_1\le 1,D_2=2]+\mathrm{Pr}[D_1=2,D_2=2]\\ & =2\cdot \frac{1}{9}\cdot \frac{1}{9}+{\frac{1}{9}}^2\\ & =\frac{2}{81}+\frac{1}{81}\\ & =\frac{3}{81}\end{array}$$ $$\begin{array}{rl}\mathrm{Pr}[X=3]& =\mathrm{Pr}[D_1=3,D_2\le 2]+\mathrm{Pr}[D_1\le 2,D_2=3]+\mathrm{Pr}[D_1=3,D_2=3]\\ & =2\cdot \frac{2}{9}\cdot \frac{1}{9}+{\frac{1}{9}}^2\\ & =\frac{4}{81}+\frac{1}{81}\\ & =\frac{5}{81}\end{array}$$ $$\begin{array}{rl}\mathrm{Pr}[X=4]& =\mathrm{Pr}[D_1=4,D_2\le 3]+\mathrm{Pr}[D_1\le 3,D_2=4]+\mathrm{Pr}[D_1=4,D_2=4]\\ & =2\cdot \frac{2}{9}\cdot \frac{3}{9}+{\frac{2}{9}}^2\\ & =\frac{12}{81}+\frac{4}{81}\\ & =\frac{16}{81}\end{array}$$ $$\begin{array}{rl}\mathrm{Pr}[X=5]& =\mathrm{Pr}[D_1=5,D_2\le 4]+\mathrm{Pr}[D_1\le 4,D_2=5]+\mathrm{Pr}[D_1=5,D_2=5]\\ & =2\cdot \frac{2}{9}\cdot \frac{5}{9}+{\frac{2}{9}}^2\\ & =\frac{20}{81}+\frac{4}{81}\\ & =\frac{24}{81}\end{array}$$ $$\begin{array}{rl}\mathrm{Pr}[X=6]& =\mathrm{Pr}[D_1=6,D_2\le 5]+\mathrm{Pr}[D_1\le 5,D_2=6]+\mathrm{Pr}[D_1=6,D_2=6]\\ & =2\cdot \frac{2}{9}\cdot \frac{7}{9}+{\frac{2}{9}}^2\\ & =\frac{28}{81}+\frac{4}{81}\\ & =\frac{32}{81}\end{array}$$

Okay now we take all the parts and get the expectation:

$$1\cdot \frac{1}{81}+2\cdot \frac{3}{81}+3\cdot \frac{5}{81}+4\cdot \frac{16}{81}+5\cdot \frac{24}{81}+6\cdot \frac{32}{81}=\frac{398}{81}$$

Question 4

This question actually exposes something interesting. Notice how the question does not specify with or without replacement when finding the sum of expectations? That’s because it doesn’t matter. I’ll sketch out the idea for why not later on.

Let $B_1,B_2$ be the random variable that have the same distribution $Pr[B=1]=\frac{1}{5}$, $Pr[B=2]=\frac{2}{5}$, $Pr[B=8]=\frac{2}{5}$. They may or may not be independent.

Now $\mathbb{E}[B_1]=\mathbb{E}[B_2]=1\cdot \frac{1}{5}+2\cdot \frac{2}{5}+8\cdot \frac{2}{5}=\frac{1+4+16}{5}=\frac{21}{5}=4.2$.

Then $\mathbb{E}[B_1+B_2]=\mathbb{E}[B_1]+\mathbb{E}[B_2]=2\cdot 4.2=8.4$

By the way, the reason why we can use this has a very important subtlety that no one has mentioned properly. Refer to these notes on LoE for a thorough explanation. It will also cover not just the subtleties behind the question but also the proof for the linearity of the expectation.

Question 5

Based on the text we have, we can get the following quantities:

$$\mathrm{Pr}[Disease]=\frac{0.1}{100}=0.001$$ $$\mathrm{Pr}[Positive|Disease]=0.85$$ $$Pr[Positive]=0.1$$

Part (a)

Now the question is asking given that it is positive, what is the probability he actually has the disease? So what we want is $\mathrm{Pr}[Disease|Positive]$. We’ll use Bayes’ theorem here:

$$\begin{array}{rl}\mathrm{Pr}[Disease|Positive]& =\frac{\mathrm{Pr}[Positive|Disease]\cdot \mathrm{Pr}[Disease]}{\mathrm{Pr}[Positive]}\\ & =\frac{0.85\cdot 0.001}{0.1}\\ & =0.0085\end{array}$$

Part (b)

Now what we instead want is $\mathrm{Pr}[Positive|\sim Disease]$.

$$\begin{array}{rl}\mathrm{Pr}[Positive|\sim Disease]& =\frac{\mathrm{Pr}[\sim Disease|Positive]\cdot \mathrm{Pr}[Positive]}{\mathrm{Pr}[\sim Disease]}\\ & =\frac{(1-0.0085)\cdot 0.1}{(1-0.001)}\\ & =0.0992\end{array}$$

Here, notice that $\mathrm{Pr}[\sim Disease|Positive]=1-\mathrm{Pr}[Disease|Positive]$. Why? Because conditioned on being positive, you either have or don’t have the disease. So the two probabilities need to sum to 1.

Question 6

There are two ways to solve this. The question first notes that some $S\in \mathcal{P}(A\times A)$ basically satisfies $S\subseteq A\times A$. Which means we can view $S$ as a relation. We are picking any relation uniformly at random. So one way of viewing this is that we get some relation $S$ with probability ${\left(2^{n^2}\right)}^{-1}$. However, I would argue this is a little cumbersome because it doesn’t tell us anything useful about what’s the probability any two $a,b$ are related with a randomly chosen $S$.

That said, if we insist on it, here’s how we’d do it.

Part (a)

For $S$ to be reflexive, we must have that $(a,a)\in S$ for all $a\in A$. So to count all subsets that satisfy this, we simply fix those $n$ possible elements of $S$, and there are $n^2-n$ remaining choices for which can either be in, or not in.

$$2^{n^2-n}\cdot 2^{-n^2}=2^{-n}$$

Part (b)

So fix any $a,b\in A$ (not necessarily distinct). Now for each of these, the moment we’ve chosen $(a,b)\in S$, then we must also have $(b,a)\in S$ (and vice versa). So now we count the number of possible sets $S$. For distinct $a,b\in A$, each of these we need to decide if both $(a,b)\in S$ and $(b,a)\in S$, or both are not in. There are also $n$ values $c\in A$ for which we need to decide if $(c,c)$ is in $S$ or not. So $\left(\genfrac{}{}{0ex}{}{n}{2}\right)+n=\frac{n(n+1)}{2}$

$$2^{\frac{n(n+1)}{2}}\cdot 2^{-n^2}=2^{-\frac{n^2-n}{2}}$$

Question 7

None of the graphs in the question are Hamiltonian since we would need to re-visit the center node more than twice.

That said, $F_1$ is Hamiltonian because:

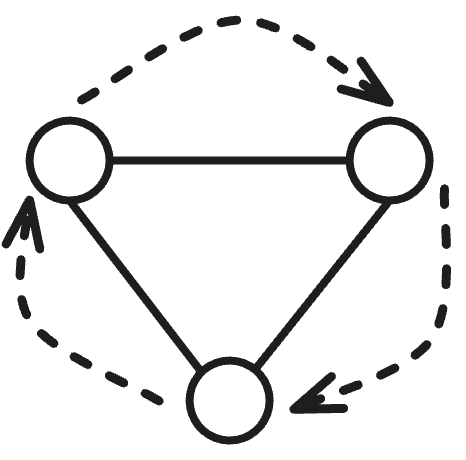
All of these graphs are Eulerian because all vertices have even degree.

Question 8

We have $2$ nodes, and $2$ edges. This means we need to pick $2$ from the set $\{1,2\}\times \{1,2\}$ with replacement. So there are $4^2=16$. Except, we don’t care about the order in which we pick the edges, and we also don’t distinguish between the two nodes (since we only want to count non-isomorphic graphs). So:

$$4^2\cdot \frac{1}{2}\cdot \frac{1}{2}=16\cdot \frac{1}{2}\cdot \frac{1}{2}=4$$

Question 9

Nothing much to say here for this question.

$$A=\left[\begin{array}{cccc}1& 0& 1& 1\\ 0& 0& 2& 1\\ 1& 2& 0& 0\\ 1& 1& 0& 0\end{array}\right]$$ $$A^0=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$ $$A^2=\left[\begin{array}{cccc}3& 3& 1& 1\\ 3& 5& 0& 0\\ 1& 0& 5& 3\\ 1& 0& 3& 2\end{array}\right]$$ $$A^3=\left[\begin{array}{cccc}5& 3& 9& 6\\ 3& 0& 13& 8\\ 9& 3& 1& 1\\ 6& 8& 1& 1\end{array}\right]$$

Part (c)

$a\to d\to b$, $a\to c\to b$, $a\to c\to b$. The last two use either $e_5$ or $e_6$.

$c\to b\to c$, using either $e_5$ then $e_6$ or the other way around. or using only $e_5$ or using only $e_6$. $c\to a\to c$.

Part (d)

$a\to a\to a\to c$ $a\to c\to a\to c$ $a\to c\to b\to c$ (where all the paths $c\to b\to c$ are taken from part $b$) $a\to d\to a\to c$ $a\to d\to b\to c$ using either $e_5$ or $e_6$.

Question 10

So we’ll go back to doing PHP here. The idea is the following: there are $n$ people, these are our vertices. Draw an edge between two vertices if the two people shook hands. The degree is the number of edges incident to that node.

So now we know there exists at least one node $v$ such that $deg(v)=n-1$ (since the host shook hands with everyone else). This also means that $\forall s[s\ne v\to deg(s)>0]$. Since everyone shook hands with the host. Also everyone’s degree is at most $n-1$ (that’s the maximum amount of people you can shake hands with).

So there are $1$ to $n-1$ possible values for the degree of each vertex, and there are $n$ vertices. So two nodes need to have the same degree (by PHP).

Question 11

I don’t think there’s much to say here so here are just some graphs that answer each part:

Part (a)

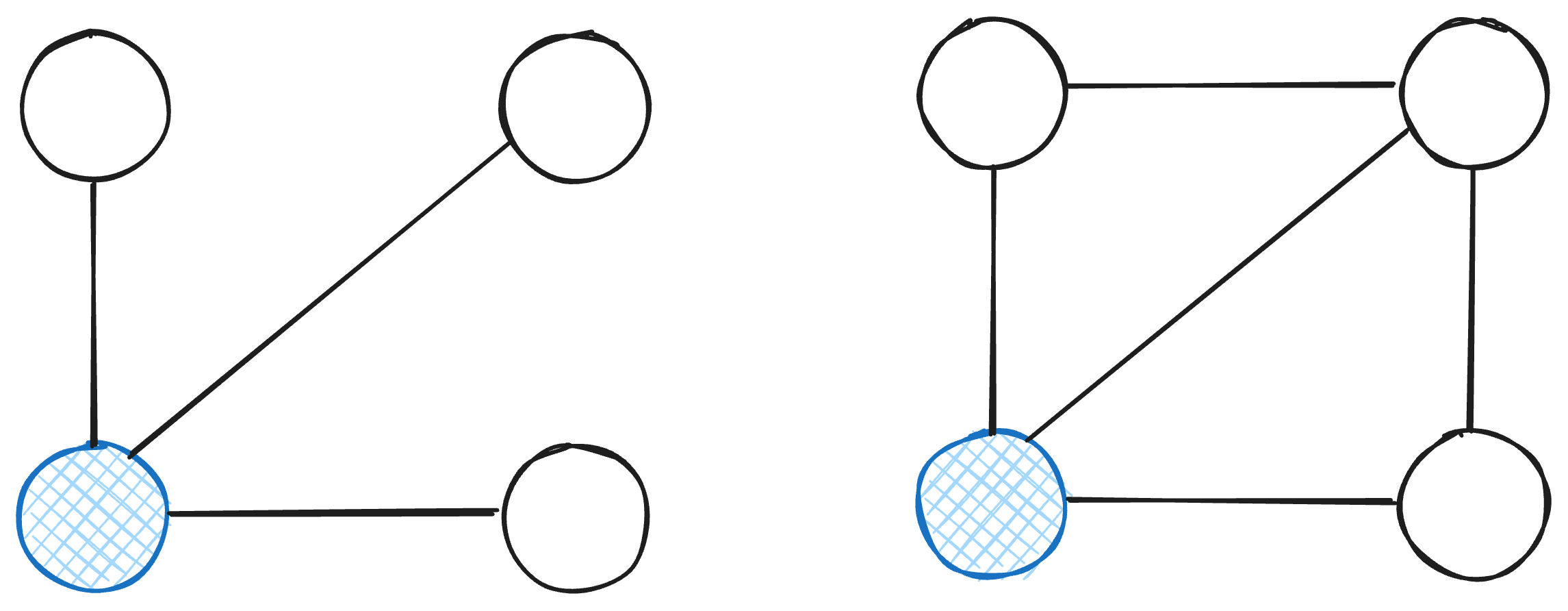
Part (b)

Question 12

Now this question is a little interesting. For newcomers to this flavour of questions might find it a bit hard because it has this “either $G$ or $\bar{G}$” kind of thing so it becomes hard to tell “oh should it be $G$ or $\bar{G}$?”

Personally when I see a question like this, one default option for me is to do the following: “I will now aim to prove if $G$ does not have any triangles, then $\bar{G}$ has at least one.” Why? Again to prove $p\vee q$ we can instead prove $\sim p\to q$ since $\sim p\to q\equiv \sim \sim p\vee q\equiv p\vee q$.

So we’ll just do that this time around as well. Though it’s a little more complicated because it’s a lot more natural for the proof to say some stuff about $G$ or $\bar{G}$ first before we do any of that stuff.

1. Consider any $v\in V$. Since there are $5$ other vertices besides $v$, let the other vertices be pigeons, and let the fact whether $v$ is incident to those vertices or not be pigeonholes.
2. There are $5$ pigeons, and $2$ holes. So now there exist $3$ vertices are either incident to $v$ or not.
3. Case 1: There exist $3$ vertices that are incident to $v$. 2. Now assume that $G$ does not have any triangles. 3. Let the $3$ vertices incident to $v$ be called $a,b,c$. 4. Since there are no triangles in $G$, this means that we cannot have $(a,b)\in E$, otherwise since $(v,a)$ and $(v,b)$ in $G$ we would already have a triangle. 5. For a similar reason, we cannot have $(b,c)\in E$, nor $(a,c)\in E$. 6. But this means that $(a,b),(a,c),(b,c)$ are edges in $\bar{G}$. 7. Then vertices $a,b,c\in V$ form a triangle in $\bar{G}$. 8. Therefore either $G$ or $\bar{G}$ has a triangle. (We assumed $G$ has no triangles and were able to conclude $\bar{G}$ has a triangle)
4. Case 2: There exist $3$ vertices that are not incident to $v$.
   1. Now assume that $\bar{G}$ does not have any triangles.
   2. Let the $3$ vertices not incident to $v$ be called $a,b,c$.
   3. Now we must have $(a,b),(a,c),(b,c)\in E$ (Why? Hint: Check case $1$ and see how to adapt that argument for case 2 instead)
   4. This means that $G$ has a triangle since vertices $a,b,c\in V$ form a triangle in $G$.
   5. Therefore either $G$ or $\bar{G}$ has a triangle. (We assumed $\bar{G}$ has no triangles and were able to conclude $G$ has a triangle)
5. In both cases it is shown that $G$ or $\bar{G}$ has a triangle.