Structural Induction

This note is organised so that we will:

1. Introduce and motivate structural induction.
2. Go through some minor differences between structural and “regular” induction.
3. Go through the tutorial questions as examples of how to use structural induction.

What is structural induction?

To see this, let’s take a step back and think about what regular induction effectively does:

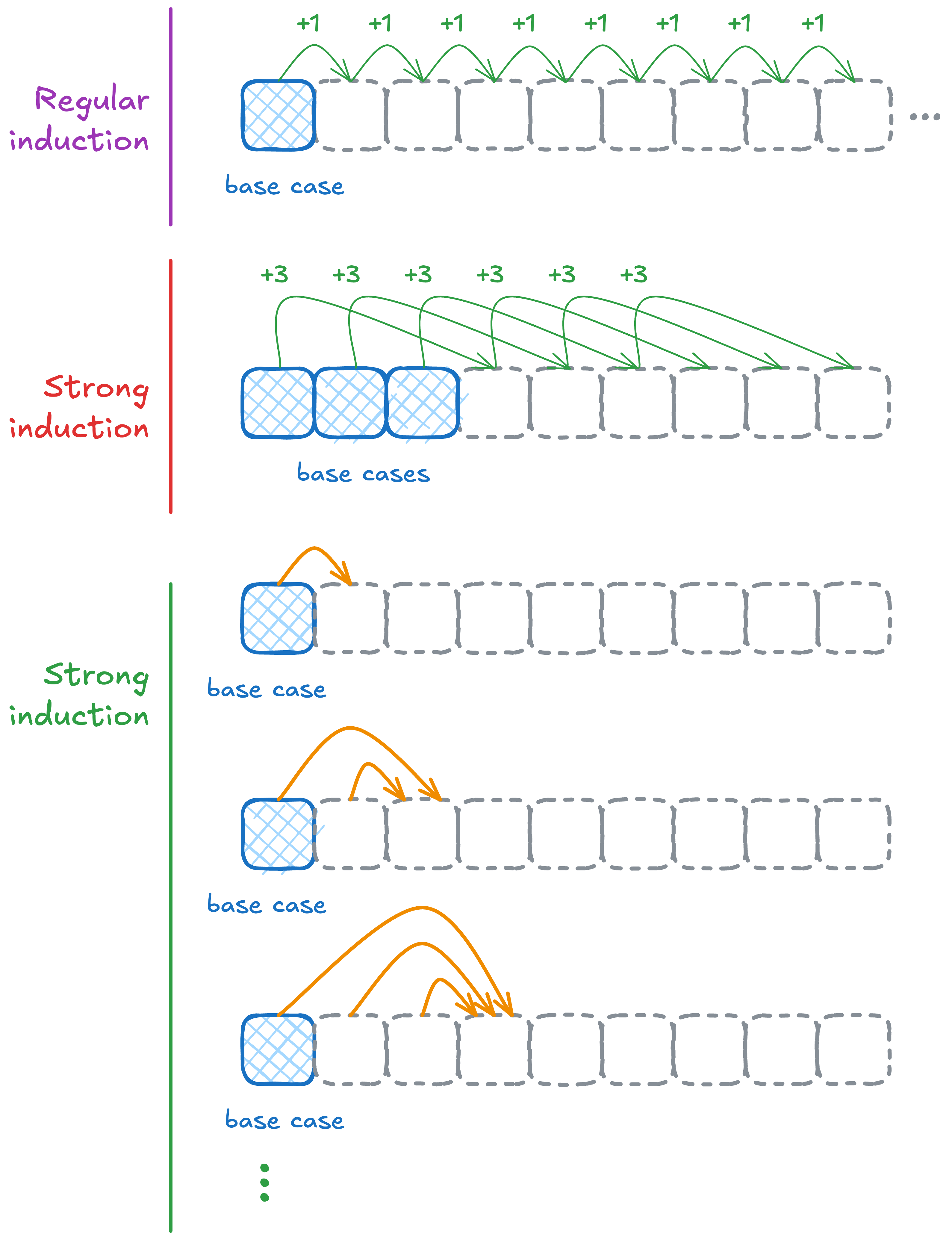
You’re basically giving a proof that says we have a starting point (our base case), and from that base case we can prove more and more cases. And typically these are an additive offset away from our base case. Like $+1$ or $+3$ or anything along those lines. Typically these induction proofs aim to prove for all $n\ge a$ where $a$ is some base case number in $\mathbb{N}$.

Recursive Structure

Structural induction is a generalised form of induction where we free ourselves from:

1. Dealing with numbers as our cases.
2. Being confined to proving statements that must be true for all $n\ge a$.

Without those constraints, it turns out we can prove a whole lot more statements. It also matches a very recursive viewpoint of a lot of the things that we know. To free ourselves up in this way, we need to define a recursive structure that we can induct on.

As a simple example, let’s say that we wanted to define set $S$ to be the set of valid mathematical expressions that involve adding numbers. So here are some examples of expressions that are valid:

1. 123
2. 123 + 412
3. 312 + 5412 + 3110

Examples of expressions that are not valid are:

1. +
2. 1 +
3. 1 ++ 2
4. + 2 + 3
5. 2 + 3 + 5 +

How would you define this? One way would be to declare set $S$ inductively in the following way:

1. $\forall x\in \mathbb{N}[x\in S]$. (Base case)
2. $\forall s_1,s_2\in S[s_1+s_2\in S]$ (Inductive case)

We’ve basically giving a recursive structure.

To be clear, the second clause is basically saying that if you can give me two valid expressions from $S$, then the expression that adds the two of them are also in $S$. E.g. we know that $1$ is a valid expression (base case). So $1+1$ is a valid expression (Inductive case). We also know that $2+5$ is a valid expression for similar reasons, so $1+1+2+5$ is a valid expression. So is something like $1+2+5$.

Notice this set $S$ doesn’t contain all possible strings! Only the ones we care about.

Okay that was a bit of a simplistic example, you can imagine how we might want to handle something more complicated with $+,\times ,-,÷$ though.

Note again, that this is a generalisation of the normal induction you’ve been looking at. Why? Because we can just recursively define the structure for all the natural numbers like so:

1. $0\in S$. (Base clause)
2. $x\in S\to (x+1)\in S$. (Recursion clause)
3. Membership for $S$ can always be demonstrated by (finitely many) successive applications of clauses above. (Minimality clause)

But now, we’re freed up to also do many things like reason about algorithms on lists, or trees. For example:

Example

Define a non-empty list of T to be either:

1. A pair of a T and null; Or
2. A pair of T and a list of T.

Example

Define a tree of type T is either:

1. A list of type T; or
2. A list of trees of type T.

Now we can do something like finding the maximum value of a non-empty list or summing the values in a tree and prove that our algorithm is correct. For example here’s a program that outputs the maximum value of a non-empty list:

function max(xs) {
	return is_null(tail(xs)) ? head(xs) : max2(head(xs), max(tail(xs)));
}

Similarly here’s a program that outputs the depth of a tree:

function depth(tree) {
  const depths = map(
	  elem => !is_null(elem) && !is_pair(elem) ? 0 : depth(elem), tree);
  return max(pair(0, depths)) + 1;
}

And now that we have that set up, here’s an example of how to prove your program is correct:

Claim: max(xs) correctly computes the maximum value of a list of numbers.

1. [Base Case] xs is a pair of a number and null.
   1. Then head(xs) is the number, and the maximum value in the list is also head(xs).
   2. Thus max(xs) returns the correct value in this case.
2. [Inductive Case] xs is a pair of an number, and a list tail(xs).
   1. Assume that tail(xs) is a list such that max(tail(xs)) correctly returns the maximum value of tail(xs). Let this maximum be called $m_{tail}$.
   2. Also, let $h$ be the value of head(xs).
   3. Then consider the output value of max2(head(xs), max(tail(xs))). Call it $m_{output}$.
   4. $m_{output}=\max (m_{tail},h)$ which happens to be the maximum value of the entire list.
3. Therefore max(xs) correctly computes the maximum value for all lists.

Okay that was just an idea, we actually were not too formal about what was going on. But just in case, here’s another one proving the correctness of depth.

Claim: depth(tree) correctly computes the depth of any tree.

In case you don’t know what the depth of a tree is, here’s an illustration:

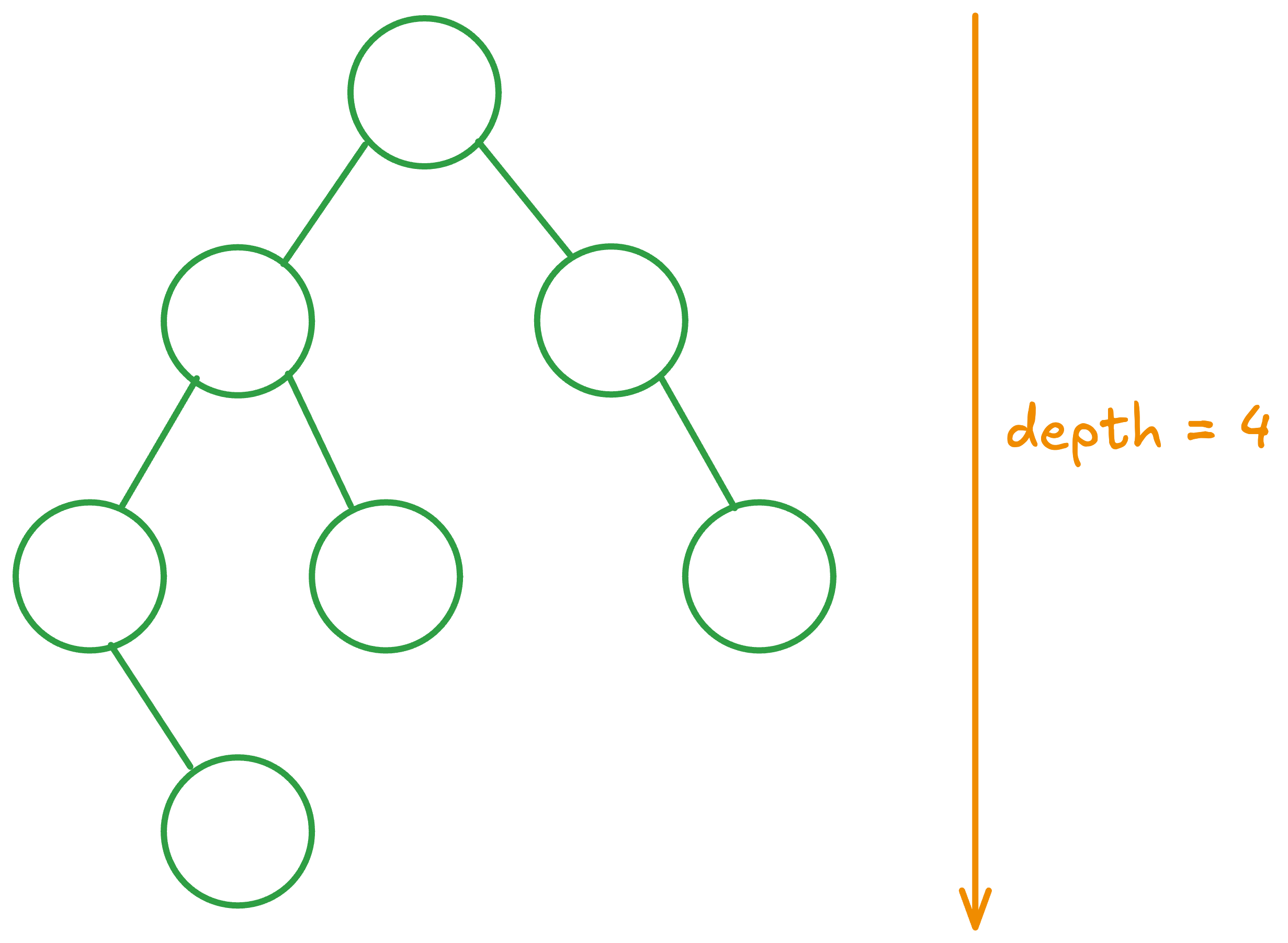
We will say trees of a single element have depth 1, and trees that have subtrees have depth that is maximum of their sub-trees + 1.

1. [Base Case] xs is a list of T.
   1. Then since T is not a pair, map(elem => !is_null(elem) && !is_pair(elem) ? 0 : depth(elem), tree); evaluates to a list of 0 or an empty list.
   2. Then max(pair(0, depths)) evaluates to $max(0,d)$ where $d$ is the maximum value of the list if it is non-empty. Which happens to be $0$. Thus the program returns $1$, which is correct.
2. [Inductive Case] xs is a list of tree of T.
   1. Then map(elem => !is_null(elem) && !is_pair(elem) ? 0 : depth(elem), tree); evaluates to a list of return values of depth on each tree.
   2. Assume that for all trees elem in xs, depth(elem) correctly computes the value of the tree represented by elem.
   3. Since we return 1 + max(pair(0, depths)), this by definition is 1 plus the maximum of the depth of our sub-trees, which is the correct value.
3. Therefore depth(tree) correctly computes the depth of any tree.

Important

These examples were perhaps a little straightforward but if anything, you shouldn’t take this as a sign that it means we don’t need to prove our programs are correct. If anything, it’s rather the case that it’s possible to write programs that are very easy to prove are correct.

In fact, one amazing aspect about functional programming (and without side effects) is precisely the case that doing things recursively on recursive structures allows you to very easily reason about the correctness of your program without having to write a formal proof because the code already mirrors the proof.

Tutorial question as an example

Hamming Numbers

Consider the following set:

$$H=\{x:\exists i,j,k\in \mathbb{N}[x=2^i\cdot 3^j\cdot 5^k]\}$$

Instead of defining it this way, consider this following (equivalent) definition:

1. $1\in H$
2. If $n\in H$, then $2n\in H$, and $3n\in H$, and $5n\in H$.
3. For any $n$, membership in $H$ can always be demonstrated by finitely many applications of the above clauses.

So with the alternative definition, we want to claim that if you took any $n$ in the set $H$ (that was recursively defined), it has a unique representation in the form of $2^i\cdot 3^j\cdot 5^k$.

Bear in mind here, that I’ve told you the two definitions are equivalent without proving it. So in some sense you can also think of this as partly proving that the two definitions are indeed equivalent (actually our proof will do a little more than that).

So, as before, we’ve given $H$ a recursive structure. So we should induct on the structure of $H$.

1. [Base Case] Consider $n=1$.
   1. $1=2^0\cdot 3^0\cdot 5^0$.
   2. Therefore, exists $i,j,k\in \mathbb{N}$ such that $1=2^i\cdot 3^j\cdot 5^k$. (Existential Generalisation)
   3. Furthermore, assume exists $x,y,z\in \mathbb{N}$ such that $1=2^x\cdot 3^y\cdot 5^z$. Then since $x,y,z$ must be $0$ otherwise, $2^x\cdot 3^y\cdot 5^z>1$.
   4. Therefore $i=j=k=0$ is the unique sequence of values for which $1=2^i\cdot 3^j\cdot 5^k$.
2. [Inductive Case] Let $n\in H$, arbitrarily chosen. Further assume that $n$ has unique values $i,j,k\in \mathbb{N}$ such that $n=2^i\cdot 3^j\cdot 5^k$.
   1. Consider $2n$. Then $2n=2^{i+1}\cdot 3^j\cdot 5^k$. Thus exists values $i^{\prime },j^{\prime },k^{\prime }\in \mathbb{N}$ such that $2n=2^{i^{\prime }}\cdot 3^{j^{\prime }}\cdot 5^{k^{\prime }}$.
   2. Furthermore, assume exists $x,y,z\in \mathbb{N}$ such that $2n=2^x\cdot 3^y\cdot 5^z$. Then $2^x\cdot 3^y\cdot 5^z=2^{i^{\prime }}\cdot 3^{j^{\prime }}\cdot 5^{k^{\prime }}$. And $\frac{2^x\cdot 3^y\cdot 5^z}{2^{i^{\prime }}\cdot 3^{j^{\prime }}\cdot 5^{k^{\prime }}}=1$.
   3. Assume for the sake of contradiction that at either: $x\ne i^{\prime }$, $y\ne j^{\prime }$, $z\ne k^{\prime }$, then it must be that $1=2^a\cdot 3^b\cdot 5^c$ where at least one of $a,b,c\in \mathbb{Z}$ is non-zero.
   4. But then that is a contradiction since $2,3,5$ are all prime so it must be that $2^a\cdot 3^b\cdot 5^c\ne 1$.
   5. Therefore $x=i^{\prime },y=j^{\prime },z=k^{\prime }$ and thus the values are unique.
   6. The arguments for $3n$, and $5n$ work similarly. (This is where you’d use WLOG)
3. Thus, for all $n\in H$, exists unique $i,j,k\in \mathbb{N}$ such that $n=2^i\cdot 3^j\cdot 5^k$.

Showing all sorts of properties on recursively defined sets

Consider the following set $S$:

1. $2\in S$
2. If $x\in S$ then $3x\in S$ and $x^2\in S$.
3. For any $n$, membership in $S$ can always be demonstrated by finitely many applications of the above clauses.

It’s probably doable to show that $2,6,16,36$ are in $S$. Why? Because:

1. $2\in S$ due to the base clause.
2. $\therefore 4\in S$ because $2\in S$ and thus $2^2\in S$.
3. $\therefore 16\in S$ because $4^2$ and thus $4^2\in S$.
4. $6\in S$ because $2\in S$ and thus $3\cdot 2\in S$.
5. $36\in S$ because $6\in S$ and thus $6^2\in S$.

But how do we show $0$ and $15$ aren’t in $S$? We will want to show some properties about $S$. To do this, since $S$ was defined recursively, we need to also use structural induction to prove that these properties indeed hold about all elements of $S$.

E.g. we want to argue that $\forall x\in S[x\ge 2\wedge x\text{ is even}]$.

1. [Base Case] Consider $n=2$.
   1. Since $2\ge 2$ and $2$ is even, $n\ge 2\wedge n\text{ is even}$.
2. [Inductive Case] Let $n\in S$, arbitrarily chosen. Further assume that $n$ is even, and $n\ge 2$.
   1. Now consider $3n$. Since $n$ is even, $n=2k$, $\exists k\in \mathbb{Z}$. Thus $3n=3\cdot 2\cdot k$. Thus $3n=2k^{\prime }$, where $k^{\prime }=3k\in \mathbb{Z}$.
   2. Also, $3n\ge 3\cdot 2\ge 2$.
   3. Thus, $3n$ is even, and $3n\ge 2$.
   4. Now consider $n^2$. Since $n$ is even, $n=2k$, $\exists k\in \mathbb{Z}$. Thus $3n=3\cdot 2\cdot k$. Thus $k^2=2\cdot (2\cdot k^2)$, where $2k^2\in \mathbb{Z}$.
   5. Also, $k^2\ge 2^2\ge 4\ge 2$.
   6. Thus, $n^2$ is even, and $3n\ge 2$.
3. Thus for all $n\in S$, $n$ is even, and $n\ge 2$.

Upon proving this, we know that $15$ and $0$ cannot be in $S$ because if they were, then they would have been even and greater than or equals to $0$.

Showing all sorts of properties on recursively defined sets (example 2)

1. $\{1,2,3,4,5\},\{1,3,5,7,9\}\in S$
2. If $X,Y\in S$ then $X\cap Y\in S$, $X\cup Y\in S$, $X\setminus Y\in S$,
3. For any $X$, membership in $S$ can always be demonstrated by finitely many applications of the above clauses.

So again, something like $\{2,4,7,9\}$ can be shown to be in $S$. Because $\{2,4\}=\{1,2,3,4,5\}\setminus \{1,3,5,7,9\}$, and $\{7,9\}=\{1,3,5,7,9\}\setminus \{1,2,3,4,5\}$.

But what about $\{2,3,4,5\}$?

What we want to argue is that for all sets $X\in S$ , elements $1,3$ must either both be in $X$, or both not be in $X$. I.e. $\forall X\in S[1\in X⟺3\in X]$.

1. [Base Cases]
   1. We know it’s true for both $\{1,2,3,4,5\}$ and $\{1,3,5,7,9\}$.
2. [Inductive Case]
   1. Let $X,Y\in S$, assume that $1\in X⟺3\in X$, and $1\in Y⟺3\in Y$.
   2. Consider $X\cup Y$. Now either (1) at least one of $X$ or $Y$ has both of $1$ and $3$ or (2) both of them do not have $1$ and $3$. (It’s only these two cases because of our assumption)
      1. If at least one of $X$ or $Y$ has both $1$ and $3$, then $X\cup Y$ has both $1$ or $3$. I.e. $1\in X\cup Y⟺3\in X\cup Y$.
      2. If both of them do not have both $1$ and $3$, then $X\cup Y$ has neither $1$ nor $3$. I.e. $1\in X\cup Y⟺3\in X\cup Y$.
   3. Consider $X\cap Y$. Now either (1) both of $X$ and $Y$ has both of $1$ and $3$ or (2) at most one of $X,Y$ has both $1$ and $3$. (It’s only these two cases because of our assumption)
      1. If both of $X$ and $Y$ has both of $1$ and $3$, then $X\cap Y$ has both $1$ and $3$. Therefore $1\in X\cap Y⟺3\in X\cap Y$.
      2. If at most $X$ or $Y$ has both of $1$ and $3$, then $X\cap Y$ does not have neither $1$ nor $3$. Therefore $1\in X\cap Y⟺3\in X\cap Y$.
   4. Consider $X\setminus Y$. (This gets a little case bashy).
      1. Case 1: $X,Y$ has both $1,3$
         1. Then $X\setminus Y$ does not have either $1$ nor $3$.
      2. Case 2: $X$ has both $1,3$, but $Y$ does not either $1$ nor $3$.
         1. Then $X\setminus Y$ has both $1$ and $3$.
      3. Case 3: Either $X$ does not have $1,3$ or $Y$ has $1,3$.
         1. Then $X\setminus Y$ does not have either $1$ nor $3$.
      4. Therefore in all cases $1\in X\setminus Y⟺3\in X\setminus Y$
3. Thus in all cases, for all $X\in S[1\in X⟺3\in X]$.

With that, we can argue that $\{2,3,4,5\}$ is not in $S$ because it contains $3$ but not $1$.