Set Cardinality, Infinity, and The Halting Problem

In our journey of formalising everything that we know, let’s reinspect something that we’ve taken for granted: Set sizes. Thus far we’ve sort of been eyeballing it for finitely sized sets. E.g. $A=\{1,2,5\}$ so we say that $|A|=3$. So how do we say $|A|<|B|$? We’d probably say $|A|=s_A,|B|=s_B$ with $s_A,s_B\in \mathbb{N}$. Then if $s_A\le s_B$, then we know $|A|\le |B|$.

But here, there are many things that actually have been left unformalised, and also unsolved. For example:

1. Okay let’s say we accept that we can compare two natural numbers for free (which actually can be formalised, but story for another day).
2. How do we rigorously say that the size of a set $|A|=n$? You might say “I can just list them out and count.” but sometimes that’s not enough for mathematicians.
3. Even more worryingly, we’ve only talked about finite sets. What about infinite sets? You could count until the cows come home and never be done.
4. Is there only one infinity? We all know that $\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}$ all behave a little different. $\mathbb{N}$ seems to only be infinite in one way, $\mathbb{Z}$ seems to be infinite in two ways, $\mathbb{Q}$ seems to be so infinite, you can take two items and find infinitely many items between them (where “between” is based on the $<$ relation). $\mathbb{R}$ seems to be so infinite it even contains infinitely many more items that $\mathbb{Q}$ does not. But are their “sizes” different?

So let’s talk about how to formalise these things and study not just counting the sizes of finite sets, but the sizes of infinite sets, and see how infinity behaves.

Question

Isn’t this a little too abstract? Why do I need to know this in computer science?

I’m glad you asked! So later on when we understand diagonalisation and the different infinities better, I’m going to show you how we can formally prove that there exists problems out there that computers cannot solve.

In fact, as newcomers (or not) to programming, you might wonder: Can my compiler/runtime environment ever look at my code and tell me it will loop forever, and then I can go fix it. The answer is nope. To be clear, it might be able to spot certain patterns and warn you, but there isn’t a perfect algorithm that has 100% accuracy on this. We’ll see this at the end of the notes.

Disclaimer

The following notes are not meant to be a formal foray into set theory and the cardinals. So we will be glossing over a lot of details (for convenience) and taking a lot of very hardcore theorems for granted. So to be clear we’re restricting ourselves to certain statements we want to make. And the focus of these notes is to just give intuition on higher level ideas about stuff between sets.

Let’s begin!

Our starting point is picking up where we let off with functions. So recall:

Pigeonhole Principle and Why Use Functions to Count

So our starting point is to start with how to “formalise” comparing set sizes. We will use functions. Recall:

A function $f:A\to B$ is:

1. Injective, if and only if, $\forall a_1,a_2\in A[f(a_1)=f(a_2)\to a_1=a_2]$
2. Surjective, if and only if, $\forall b\in B,\exists a\in A[f(a)=b]$
3. Bijective, if and only if, $f$ is both injective and surjective.

Important Disclaimer

Full disclaimer: I had to debate with myself for over weeks what exactly I should show you in these notes. I either have a natural and usable sequence that shows you how this all naturally fits in together but run the risk of you using theorems out of syllabus (which would not be accepted) or I stick with the very limited set of theorems that they’ve given you in CS1231S. Then our hands are tied behind our back and the exposition makes no sense. So for this section (the one titled Pigeonhole Principle and Why Use Functions to Count) I will do the following: I will mark the theorems and statements that are out of syllabus. My rationale for mentioning it is that they’re insanely intuitive anyway, and I want to appeal to your sense of intuition on how to navigate this tricky topic. The tradeoff is: You are not allowed to take the out-of-syllabus theorems and statements for use in CS1231S. If you quote Schroder-Bernstein etc, we have tutors that will understand you, but there’s no guarantee it will be accepted. But it’s not in the slides.

Let’s say I had two sets, and I wanted to say one was “at most the size” of the other. How should I do that? You see if we had finite sizes we can kind of count it. If there was only one kind of infinite size, we could then also just have happily declared “ok all infinite sizes are the same”, and finite sizes can be compared. Except.. the world doesn’t work that way. There are many infinite sizes, and also at the same time, when the world of mathematics started being formal around the mid 1800s, the community was finding ways to construct numbers from sets. It was easy to believe that sets are an intuitive concept we’re happy to accept exist (as a philosophical choice) and it was actually quite easy to construct numbers from sets. On the other hand, it was very hard to construct sets from assuming numbers exist. This sort of led us to actually build the foundation of mathematics based on the existence of sets. It’s very trippy that we can assume sets exist and then say “therefore numbers exist”. But it’s true!

So put yourself in the shoes of an 1850’s mathematician. Right now, you’re not allowed to assume numbers exist, and you have to construct them if need be. How should you argue that $|A|\le |B|$?

Aside

Notice here I am saying that the $|A|$ here cannot actually yet mean a number. We must take two sets $A,B$ and then surround them by $|$, and then this thing can sandwich a $\le$ symbol if and only if there exists an injection $f:A\to B$.

So at least in the current formalisation: We can only compare set sizes, and we can only argue set cardinalities relatively between $A$ and $B$. We cannot say $|A|=n$ for some $n\in \mathbb{N}$.

The most natural solution (hah get it? Natural) was to just give a function $f:A\to B$ that was injective. What’s the idea? You know that functions are actually just sets. Okay so they exist. Moreover, there’s a philosophical interpretation going on here:

Since for every element in $A$, I can find a unique “item” for it in $B$, this means that the number of items in $A$ are at most the number of items in $B$. Otherwise, my function $f$ would have had to make two distinct elements of $A$ share the same item in $B$.

Running with that same idea, philosophically speaking, can’t we also say the same if we had a surjection? Why indeed yes we can.

So if you gave a function $g:B\to A$ that is surjective instead, you can also conclude $|A|\le |B|$.

Since for every element in $A$, I can find at least one for it in $B$ (could be more than one), this means that the number of items in $B$ are at least the number of items in $A$. Otherwise, my function $g$ should sort of fail to cover at least one element in $A$.

To be clear, to show the statement $|A|\le |B|$, you can either give an injection $f:A\to B$ or a surjection $g:B\to A$. Either is good.

Now lastly, to argue two sets have the same size, we can give a bijection $h:A\to B$ to argue that $|A|=|B|$. The philosophical interpretation works the same.

Out of Syllabus

But wait. If I gave two injections $f:A\to B$, and $g:B\to A$ can’t we also say $|A|=|B|$? Because $f$ says that $|A|\le |B|\le |A|$.

Yes. Yes you can.

…So you’re telling me, if I have $f:A\to B$, and $g:B\to A$ both injective functions, then there exists a bijection $h:A\to B$?

Yes! This is called the Cantor-Schroder-Bernstein theorem.

The below theorem is out of syllabus.

Theorem

(Cantor-Schoder-Bernstein) If there exists injective functions $f:A\to B$, $g:B\to A$ between sets $A,B$. Then there exists bijective function $h:A\to B$.

We’ve also not talked about how set cardinalities form a total order. That is to say: any two set cardinalities can be compared. In fact (for your intuition but it’s out of syllabus to use this):

Theorem

Let $A,B$ be two sets. Then either:

1. $|A|\le |B|$; or
2. $|A|=|B|$; or
3. $|A|\ge |B|$.

And as a shorthand, we can write $|A|<|B|$ to mean $|A|\le |B|\wedge |A|\ne |B|$. That is to say, there is an injection from $A$ to be, but no bijection. You can do something similarly for $|A|>|B|$.

Using functions to talk about set cardinalities

So now hopefully you get why we’re starting with functions.

Finite Sets

So the first thing we should do is talk about finiteness. Now we can be (slightly more) formal. From this point on, we will use ${\mathbb{Z}}_n$ as a shorthand (this is not standard notation) to denote the set $\{1,2,3,\dots ,n\}=\{x:x\in \mathbb{Z}\wedge x\ge 1\wedge x\le n\}$. Also, ${\mathbb{Z}}_0$ is defined to be $\varnothing$. ¹

Then, we will say a set $A$ is finite if:

There exists an $n\in \mathbb{N}$ and a bijection function $f:A\to {\mathbb{Z}}_n$ (or equivalently, a bijection $f:\mathbb{Z}\to A$).

Intuitively, a finite set either has 0 elements, or it has $n$ elements for some $n\in {\mathbb{Z}}^{+}$. The function $f$ here is basically just telling you how to show it has $n$ elements by literally saying: “This is element 1… this is element 2…” and so on.

Infinite Sets

Countably Infinite Sets

Okay let’s move onto infinite sets because here’s where things get very interesting. And we’ll talk about the “smallest” infinity: Countable infinity. So cardinality gets a bit weirder when infinite sets are a thing. For example, $|\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}|$. In fact, let $O=\{2x+1:x\in \mathbb{N}\}$. We can also say $|O|=|\mathbb{N}|$. That seems weird, clearly there are more natural numbers than odd numbers. And perhaps you can say that. That’s why we say: the cardinalities are the same. Cardinalities are our way of talking about “size” between sets.

Technique

Let’s begin with the fundamental techinque of proving statements like: $|A|=|B|$

To prove $|A|=|B|$, in CS1231S, you need to give a bijection $f:A\to B$.

Two things to note about the additional methods (in fact, in CS1231S, they’ve mentioned this holds for finite sets): When there exists a surjection $g:A\to B$, you’re proving $|A|\ge |B|$. Does this mean you’re proving that there exists an injection $h$ from $B\to A$? Yes!

Just because there is an injection $f:A\to B$, and surjection $g:A\to B$ does not mean $f$ is a surjection, and it does not mean $g$ is a surjection. What it means is that if you prove $f,g$ exist, then there exists a bijection $h:A\to B$.

Summary

To summarise, the following are equivalent (in CS12321S):

1. $A\le B$
2. $\exists f:A\to B$ such that $f$ is injective.
3. $\exists f:B\to A$ such that $f$ is surjective.

Also, these follow are equivalent (in CS12321S):

1. $A=B$
2. $\exists f:A\to B$ such that $f$ is bijective.
3. $\exists f_1:A\to B$ and $f_2:A\to B$, such that $f_1$ is injective, and $f_2$ is surjective. (Out of syllabus)
4. $\exists f_1:A\to B$ and $f_2:B\to A$, such that $f_1,f_2$ are both injective. (Out of syllabus)
5. $A\le B\wedge B\le A$ (Out of syllabus)

Lastly, these are equivalent (in CS1231S):

1. Exists an injective function $f:A\to B$
2. Exists a surjective function $B:B\to A$

Technique

Another technique given in CS1231S that was not made entirely explicit is the following: To show $|A|\le |\mathbb{N}|$, one can give a surjective function $g:\mathbb{N}\to A$.

They’ve stated in in the form of sequences, but $g$ is basically giving you your sequence here.

Why is this simpler? Because now instead of giving a bijection, you only have to give a surjection.

For the remainder of this subsection, let’s demonstrate some of these to show some of the equalities.

And for fun, we’ll prove some of the equivalences. The proofs will be quite long but they’re collapsible so hopefully the page isn’t too large. The important point for this portion is you getting the intuition behind countably infinite. To do this I will show you how a bunch of commonly known sets are countably infinite.

Techinque

This hopefully frees you up to also use these sets “interchangeably” when showing some other set $A$ is countably infinite. The other takeaway I want you to get is notice how some of these constructions are done, because the ideas might be re-usable in other ways. So, don’t read this for the sake of “gaining knowledge” or “knowing what is true”. I need you to be able to do is observe how some of these functions are made. Then you’ll have to port some of these ideas for your own later on.

First of all, let’s ask something a little simple: What happens if I remove $0$ from $\mathbb{N}$? (I do get ${\mathbb{Z}}^{+}$) Can we show that removing $0$ from $\mathbb{N}$ still something that is the same cardinality?

Theorem

$|\mathbb{N}|=|{\mathbb{Z}}^{+}|$

Proof Idea

Consider function $f:\mathbb{N}\to {\mathbb{Z}}^{+}$ where $f:n\mapsto n+1$. This should be doable for the reader at this point, to show that this function is indeed a bijection.

Okay, how about if we had almost twice as many elements as $\mathbb{N}$? For example, what happens if we added all the negative numbers too?

Theorem

$|\mathbb{N}|=|\mathbb{Z}|$

Proof

So we’ll do this by giving the bijective function itself. Consider $f:\mathbb{N}\to \mathbb{Z}$, where $f:x\mapsto (-1{)}^x(\frac{n}{2}+\frac{1}{4})-\frac{1}{4}$ We now need to show that $f$ is bijective. We are going to employ the help of this lemma:

Claim: $f(n)$ is negative if and only if $n$ is odd.

1. Let $n\in \mathbb{N}$ be odd. I.e. $\exists t\in \mathbb{N}=2\cdot t+1$.
2. Then $(-1{)}^n=(-1{)}^{2t+1}=(-1{)}^{2t}(-1)=(-1)$
3. Then $(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1)\left(\frac{2t+1}{2}+\frac{1}{4}\right)-\frac{1}{4}$
4. $(-1)\left(\frac{2t+1}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1)(t+\frac{3}{4})-\frac{1}{4}$
5. $(-1)(t+\frac{3}{4})-\frac{1}{4}=-t-1$.
6. Since $t\in \mathbb{N},f(n)<0$.
7. Let $n\in \mathbb{N}$ be even. I.e. $\exists t\in \mathbb{N}=2\cdot t$.
8. $(-1{)}^{2t}=1$.
9. $(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}=\left(t+\frac{1}{4}\right)-\frac{1}{4}$
10. $\left(t+\frac{1}{4}\right)-\frac{1}{4}=t$
11. Since $t\in \mathbb{N}$, $f(n)=t\ge 0$.
12. By lines 6. and 10. $f(n)$ is negative if and only if $n$ is odd.

Claim: The given $f$ is surjective.

Remark: The tricky part about this one is that when we take an arbitrary $y$ as output of $f$, we don’t yet know how to argue whether $n$ is even or odd. So we begin with this first:

Now we can try to prove surjectivity.

1. Let $y\in \mathbb{Z}$ be arbitrarily chosen.
2. Either $y\ge 0$ or $y<0$.
3. Case 1: $y\ge 0$
   1. Then consider $n=2y$.
   2. Since $f(n)=(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}$
   3. $(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}=\left(y+\frac{1}{4}\right)-\frac{1}{4}$
   4. $\left(y+\frac{1}{4}\right)-\frac{1}{4}=y$
   5. Also since $2y=n$, $n\in \mathbb{N}$, by closure of $\times$ on $\mathbb{N}$.
   6. Therefore $\exists n\in \mathbb{N}[f(n)=y]$
4. Case 2: $y<0$
   1. Then consider $n=-2y-1$.
   2. $f(n)=(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}$
   3. $(-1{)}^n\left(\frac{n}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1)\left(\frac{-2y-1}{2}+\frac{1}{4}\right)-\frac{1}{4}$
   4. $(-1)\left(\frac{-2y-1}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1)(-y-\frac{1}{4})-\frac{1}{4}$
   5. $(-1)(-y-\frac{1}{4})-frac14=y$
   6. Also since $y<0$, $2y<1$, and $-2y\ge 1$, and $-2y-1\ge 0$.
   7. So $n\ge 0$.
   8. Also by closure of multiplication and subtraction/addition, $n\in \mathbb{Z}$.
   9. Therefore $n\in \mathbb{N}$.
   10. Therefore $\exists n\in \mathbb{N}[f(n)=y]$
5. In all cases it is shown that $\exists n\in \mathbb{N}[f(n)=y]$.
6. By universal generalisation, $\forall y\in \mathbb{Z},\exists n\in \mathbb{N}[f(n)=y]$.

Now we move to prove $f$ is injective.

Claim: The given $f$ is injective.

1. Let $x_1,x_2\in \mathbb{N}$ arbitrarily chosen. Further assume $f(x_1)=f(x_2)$.
2. Now, by the Lemma, either both $x_1,x_2$ are even, or $x_1,$x_2$ are odd.
3. Case 1: Both $x_1,x_2$ are even.
   1. Now $(-1{)}^{x_1}=1=(-1{)}^{x_2}$.
   2. By the assumption, $(-1{)}^{x_1}\left(\frac{x_1}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1{)}^{x_2}\left(\frac{x_2}{2}+\frac{1}{4}\right)-\frac{1}{4}$
   3. Then by line 3.1 and basic algebra: $x_1=x_2$.
4. Case 2: Both $x_1,x_2$ are odd.
   1. Now $(-1{)}^{x_1}=-1=(-1{)}^{x_2}$.
   2. By the assumption, $(-1{)}^{x_1}\left(\frac{x_1}{2}+\frac{1}{4}\right)-\frac{1}{4}=(-1{)}^{x_2}\left(\frac{x_2}{2}+\frac{1}{4}\right)-\frac{1}{4}$
   3. Then by line 3.1 and basic algebra: $x_1=x_2$.
5. In all cases it is shown that $x_1=x_2$.
6. By universal generalisation, $\forall x_1,x_2\in \mathbb{N}[f(x_1)=f(x_2)\to x_1=x_2]$.

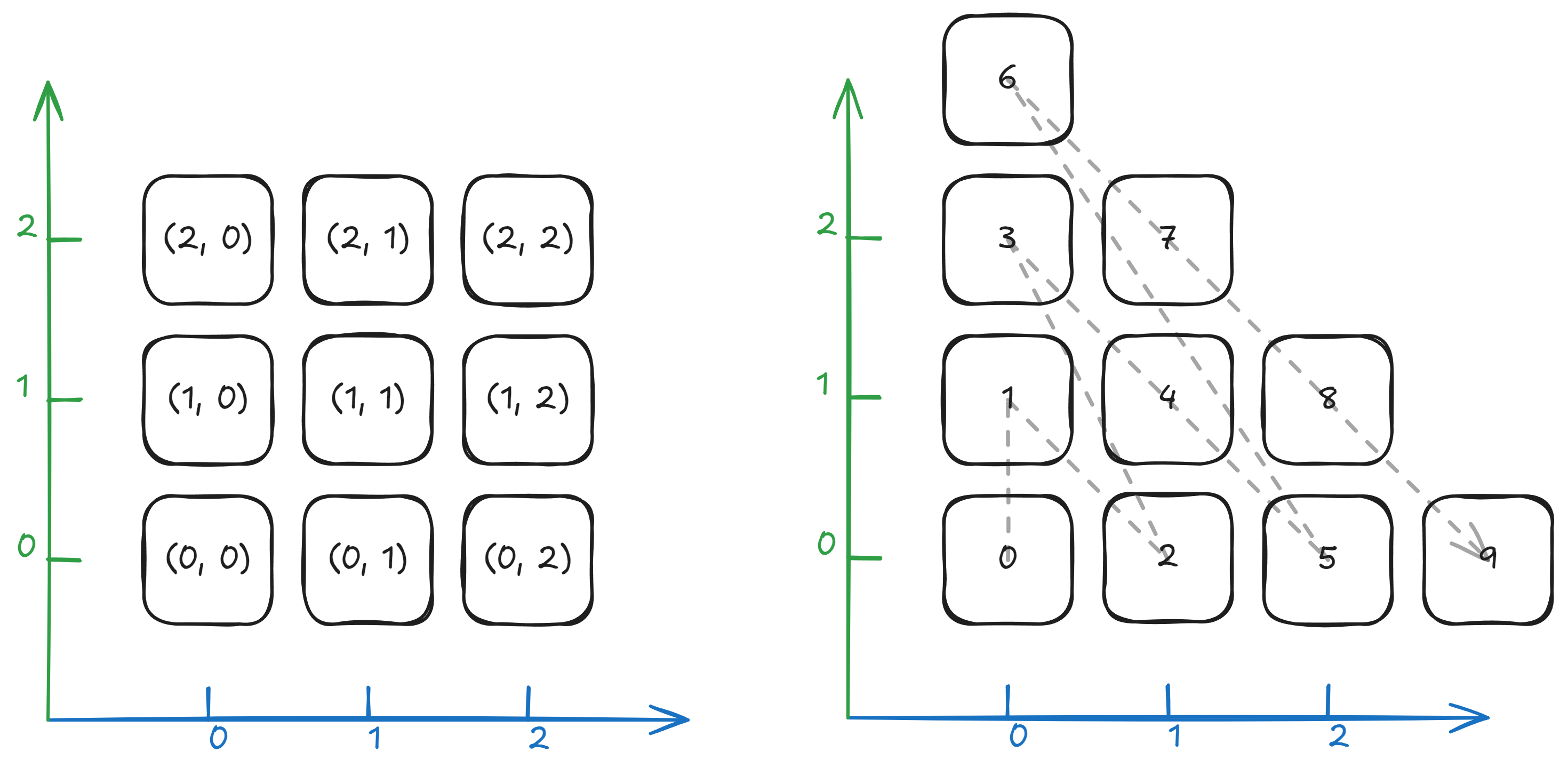
Okay, how about instead of being infinite in 1 dimension, we were also infinite in another dimension?

Theorem

$|\mathbb{N}\times \mathbb{N}|=|\mathbb{N}|$

This is one of the more useful statements. We will use what is called Cantor’s Pairing Function Here’s a proof:

Proof

Here’s a picture that sort of illustrates the what the below function is doing:

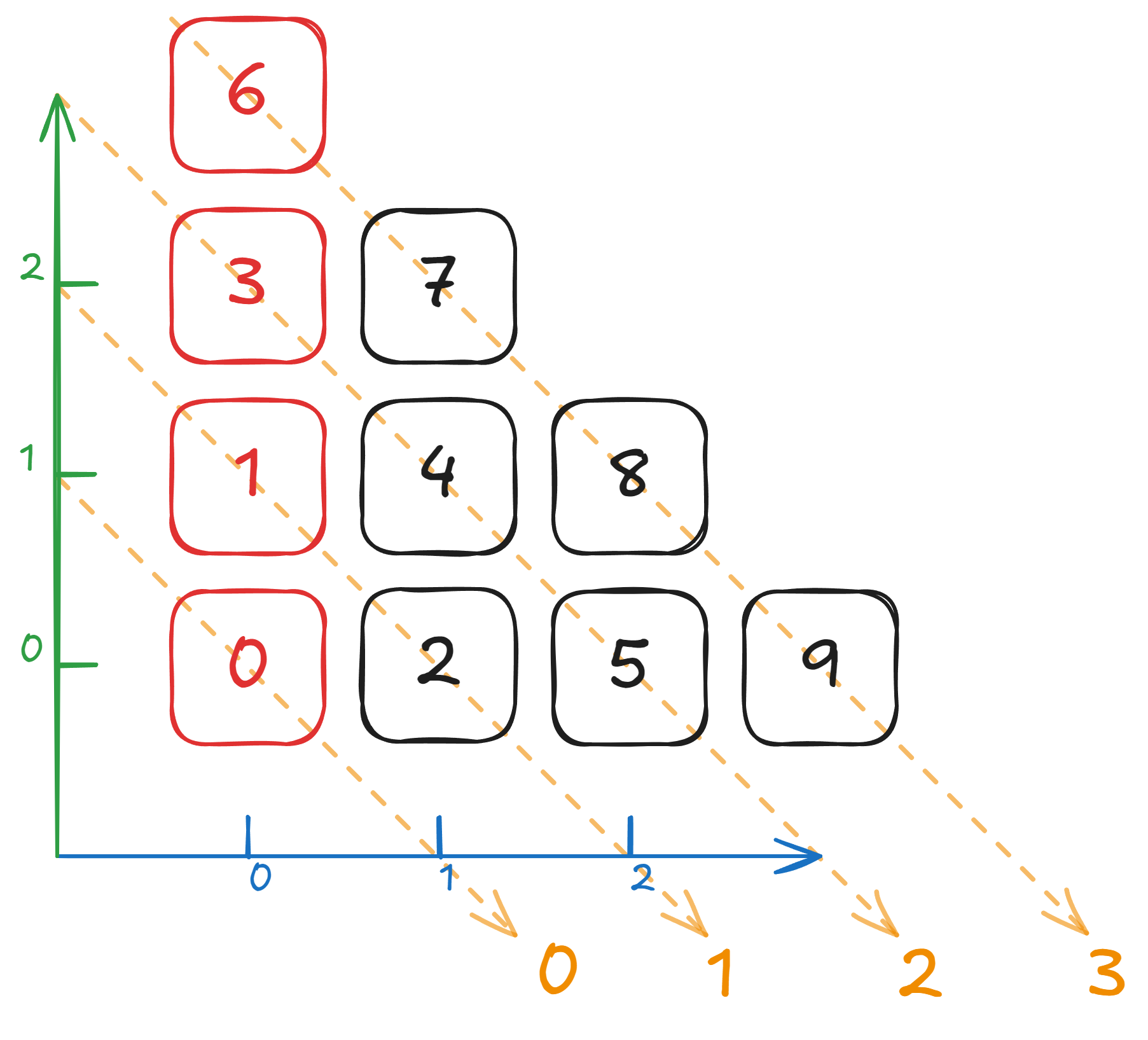
Let’s think about it this way, we’re making triangles. How do I make a $n$-tall, and $n$-wide triangle? What’s the size? It’s actually the $n^{th}$ triangle number $(n)(n+1)/2$. Try it!

One more thing, given $(i,j)$, we can actually see that it falls on the $(i+j{)}^{th}$ diagonal. We are going to refer to the $d=i+j$. So the $d^{th}$ diagonal contains all pairs $(i,j)$ such that $i+j=d$.

Combine the two ideas we had, and you can see that basically on the $d^{th}$ diagonal starts with the $d^{th}$ triangle number. Furthermore, the $d^{th}$ diagonal actually has $d+1$ elements on its diagonal. So what numbers are on the $d^{th}$ diagonal?

Any number of the form $d(d+1)/2+t$, for any $0\le t\le d$ (there are in total $d+1$ such numbers).

Okay we are in place to begin the proof. Here’s the intuition. Given $(i,j)$, we map it to the $d^{th}$ diagonal (where $i+j=d$, and its offset into the diagonal is $j$. Consider function $f:(i,j)\mapsto \frac{(i+j)(i+j+1)}{2}+j$.

We first show that $f$ is surjective. The idea is the following: We first find the largest triangle number that is at most $n$, then use that to figure out which diagonal $n$ sits on, then figure out what $n$‘s offset is on that diagonal.

1. Let $n\in \mathbb{N}$, arbitrarily chosen.
2. Let $t$ be the largest natural number such that $t(t+1)/2\le n$.
3. We first claim that $n\le t(t+1)/2+t$.
4. Suppose not. Then $n>t(t+1)/2+(t+1)-1=\frac{t(t+1)+2(t+1)}{2}-1=\frac{(t+1)(t+2)}{2}-1$.
5. Then we obtain a contradiction because now $t+1>t$, and $n\ge \frac{(t+1)(t+2)}{2}$.
6. Now consider $j=n-t(t+1)/2$. Since $n\le t(t+1)/2+t$, $j\le t$.
7. Also since $n\ge t(t+1)/2$, $j=n-t(t+1)/2\ge 0$.
8. Now let $i=t-j$. Since $j\le t$, $i\ge 0$.
9. Now both $i,j\in \mathbb{N}$, since $t\in \mathbb{N}$.
10. Now $f(i,j)=\frac{(i+j+1)(i+j)}{2}+j$ $=\frac{(t+1)(t)}{2}+n-\frac{t(t+1)}{2}$ $=n$
11. Therefore, $\forall n\in \mathbb{N},\exists i,j\in \mathbb{N}[f(i,j)=n]$.

Remark: To be clear, in case the argument looks circular, the important idea is the following: when we are given $n$, we need to figure out which diagonal it’s on. To do this, we needed to find the largest triangle number that is less than or equals to $n$. Let that be the $t^{th}$ triangle number. Then we know $n$ was due to some $i,j$ such that $i+j$ is $t$. Then, to figure out $j$, we know $n$ is exactly $j$ away from $t(t+1)/2$. So $j=n-t(t+1)/2$. We then had to check that $i$ and $j$ were natural numbers. I.e. $\ge 0$, and I skipped a few steps on closure. E.g. $t(t+1)/2$ is a natural number. But that’s the idea.

Next, we show that $f$ is injective. To do this, we again use the fact that we can compare two outputs using which diagonal they are sitting on. If it’s different, they we know they’re already different. If they’re the same, then their offsets into the diagonal must be different. To do this, we will actually prove the contrapositive statement.

1. Let $(i_1,j_1),(i_2,j_2)\in \mathbb{N}\times \mathbb{N}$. Further assume that $(i_1,j_1)\ne (i_2,j_2)$.
2. Either $i_1+j_1=i_2+j_2$, or $i_1+j_1\ne i_2+j_2$.
3. Case 1: $i_1+j_1=i_2+j_2$
4. Letting $i_2+j_2=d=i_1+j_1$:
5. Assume that $j_1=j_2$.
   1. Then $i_2=d-j_2=d-j_1=i_1$.
   2. Then $j_1=j_2$ and $i_1=i_2$. Contradiction against line 1.
6. Therefore $j_1\ne j_2$
7. $f(i_1,j_1)=(d)(d+1)/2+j_1$
8. $\ne (d)(d+1)/2+j_2$
9. $=f(i_2,j_2)$
10. Therefore, $\forall (i_1,j_1),(i_2,j_2)\in \mathbb{N}\times \mathbb{N}[(i_1,j_1)\ne (i_2,j_2)\to f(i_1,j_1)\ne f(i_2,j_2)]$
11. $f$ is injective (Contrapositivity of line 4).

We will save $\mathbb{N}$ vs $\mathbb{Q}$ for a little later on.

Within Countable Infinity

It turns out we have a name for the “size” or cardinality of $\mathbb{N}$. We call it ${\aleph }_0$ (pronounced “aleph null”). This is the first transfinite cardinal number. Think of cardinal numbers as “numbers” that represent the size of sets. So we write $|\mathbb{N}|={\aleph }_0$.

Definition

We will say a set $A$ is countably infinite if $A$ has a bijection to $\mathbb{N}$.

Furthermore, we will say a set $A$ is countable if either:

1. $A$ is finite; Or
2. $A$ is countably infinite.

It’s important to note the difference between countable and countably infinite.

That said, there is a different formulation that I’ve previously mentioned. Basically:

Remark

A set $A$ is countable if there exists a surjective function $f:\mathbb{N}\to A$.

The CS1231S treatment is via sequences. But such a function $f$ that is surjective basically provides a sequence that satisfies their lemma 9.2.

There are a few useful facts (provable theorems, in fact) that you should know. Let’s list some out now:

1. $|\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}|={\aleph }_0$
2. Let $A,B$ be disjoint, countable sets. Then $A\cup B$ is countable.
3. Let $A\subseteq B$ where $B$ is countably infinite. Then $A$ is countable.
4. If $A,B$ are countably infinite sets, then $|A\times B|=|A\cup B|={\aleph }_0$.
5. If $A,B$ are countable sets. Then $A\times B$ is countable. Also, $A\cup B$ is countable.
6. Let $A_1,A_2,\dots =(A_n{)}_{n\in {\mathbb{Z}}^{+}}$ be a sequence of countable sets. Define ${\bigcup }_{i=1}^{\infty }{A}_i=\mathcal{A}$. Then $\mathcal{A}$ is countable.

We’re going to try proving these statements. What I want you to think of it is more of us developing the tooling to argue about even more theorems. Also, I think some of these statements might be useful as lemmas. Also it would be good if you at least think about how to prove these statements first before comparing it against my proof to see if there’s any subtlety you’ve left out.

Before we do this, it’s going to be helpful to be able to union two sets. Now normally I would just show you how to do it via a bijection (just in case). There’s many variations of these, we’ll work up to them slowly because we can bootstrap our previous results to build bigger and bigger theorems.

Mini Tooling:

Let’s begin!

We’re going to union two countably sets, and show that they’re countable. There are many variants, and because we’re insisting on bijections (rather than surjections), the proofs all look a little different.

Let $A,B$ be sets. $A$ is countably infinite and $B$ is finite. Further assume $A,B$ are disjoint. Then there exists a bijection $f:{\mathbb{Z}}^{+}\to (A\cup B)$.

So here’s the idea, since they’re disjoint, we can just list out the elements of $B$ first, then the elements of $A$, since they don’t overlap, setting $g(1)=b_1$, …, $g(t)=b_t$ where $t$ is the cardinality of finite $B$. Then after that $g(t+1)=a_1,g(t+2)=a_2,\dots$.

1. Let $A,B$ be disjoint. $A$ countably infinite, and $B$ be finite.
2. Since $A$ is countably infinite, there exists a bijection $f_A:{\mathbb{Z}}^{+}\to A$.
3. Since $B$ is finite, there exists $t\in \mathbb{N}$ such that $f_B:{\mathbb{Z}}_t\to B$.
4. We are now in place to construct a bijection $g:{\mathbb{Z}}^{+}\to A\cup B$.
5. Let $n\in {\mathbb{Z}}^{+}$, then:

$$g(n)=\{\begin{array}{ll}{f}_B(n),& \text{ if }n\le t\\ f_A(n-t),& \text{ if }n>t\end{array}$$

Now of course one can eye-ball it to say it’s injective and surjective. And if we are going to do that for all the notes, these notes are never going to finish. So I propose the following, I will do it for this one. For the rest, you can and should take it as practice in showing functions are bijective.

Claim 1: $g$ is surjective.

1. Let $y\in A\cup B$, arbitrarily chosen. Then either $y\in A$ or $y\in B$ but not both. (Since they are disjoint)
2. Case 1: $y\in A$.
   1. Then since $f_A$ is bijective, $f_A$ is surjective.
   2. Therefore, there is an $i\in {\mathbb{Z}}^{+}$ such that $f_A(i)=y$.
   3. Now $g(i-t)=f_A(i)$ (Since $i>t$, by domain of $f_A$)
   4. Then $f_A(i)=y$ (By definition of $f_A$)
3. Case 2: $y\in B$.
   1. Then since $f_B$ is bijective, then $f_B$ is surjective.
   2. Therefore, there is a $i\in {\mathbb{Z}}_t$ such that $f_B(i)=y$.
   3. Now $g(i)=f_B(i)$ (Since $i\in {\mathbb{Z}}_t$)
   4. Then $f_B(i)=y$ (By definition of $f_B$).
4. Thus in all cases it is shown that $\exists n\in {\mathbb{Z}}^{+}[g(n)=y]$
5. Therefore, $\forall y\in A\cup B\exists n\in {\mathbb{Z}}^{+}[g(n)=y]$.

Claim 2: $g$ is injective.

1. Let $x_1,x_2\in mathbb{Z}^{+}$ arbitrarily chosen. Further assume $g(x_1)=g(x_2)$.
2. Now let $z\in A\cup B$ such that $z=g(x_1)=g(x_2)$.
3. Either $z\in A$ or $z\in B$.
4. Case 1: $z\in A$
   1. Then $z\notin B$ ($A,B$ disjoint.)
   2. Therefore $z$ is not in the range of $f_B:{\mathbb{Z}}_t\to B$.
   3. Since $f_A$ is bijective, exists a unique $x$ such that $f_A(x)=z$.
   4. Since $f_A(x)=f_A(x_1)$, then $x_1=x$.
   5. Since $f_A(x)=f_A(x_2)$, then $x_2=x$.
   6. Therefore $x_1=x_2$.
5. Case 2: $z\in B$
   1. Then $z\notin A$ ($A,B$ disjoint.)
   2. Then $z$ is not in the range of $f_A:{\mathbb{Z}}^{+}\to A$
   3. Since $f_B$ is bijective, there exists a unique $x$ such that $f_B(x)=z$.
   4. Since $f_B(x)=f_B(x_1)$, then $x_1=x$.
   5. Since $f_B(x)=f_B(x_2)$, then $x_2=x$.
   6. Therefore $x_1=x_2$.
6. In all cases it is shown that $x_1=x_2$.
7. Therefore $\forall x_1,x_2\in {\mathbb{Z}}^{+}[g(x_1)=g(x_2)\to x_1=x_2]$.

Okay, so we’ve done the simplest case when $A$ is countably infinite, $B$ is finite, and they are disjoint. Let’s try something a few more involved ones. From now on I’ll give you the functions, and you need to prove it yourself that they’re bijections.

Let $A,B$ be disjoint sets. Both $A,B$ are countably infinite. Then $A\cup B$ is countably infinite.

1. Since $A$ is countably infinite, then there exists a bijection $f_A:{\mathbb{Z}}^{+}\to A$.
2. Since $B$ is countably infinite, then there exists a bijection $f_B:{\mathbb{Z}}^{+}\to B$.
3. Consider function $g:{\mathbb{Z}}^{+}\to A\cup B$: $g:n\mapsto \{\begin{array}{ll}{f}_A((n+1)/2)& ,\text{ if }n\text{ is odd}\\ f_B(n/2)& ,\text{ if }n\text{ is even}\end{array}$

Claim: $g$ is a bijection.

Okay we’ve dealt with the two cases but with the nice assumption that they’re disjoint. What about if they’re not disjoint? Then things get a bit more annoying. But remember we’re free now to use these 2 above statements as lemmas to help us prove the non-disjoint cases. Again I’ll give you guys a proof idea, and try to finish the proof by giving a bijection $g$.

It’s going to be helpful to have this lemma:

Lemma

1. Let $B$ be countably infinite. Then any subset $A$ of $B$ is countable.
2. Let $C$ be finite, then any subset $D$ of $C$ is finite.
3. Let $A$ be countably infinite, and $B$ be finite. Then $A\setminus B$ is countably infinite.

Let $A\subseteq B$ where $B$ is countably infinite. Then $A$ is countable.

The idea is to use the fact that there exists a surjection $g$ from $\mathbb{N}$ to $B$, to create another surjection $\mathbb{N}$ to $A$. Now the tricky part is the following: What do we do about the elements $n\in \mathbb{N}$ where $g$ maps to outside of $A$ but is still in $B$?

To deal with this we need to case break a little. If $A$ is empty, then it’s finite, so we don’t have to do anything, that’s by definition countable. If $A$ is not empty, then it has at least one element. Now any $n$ that $g$ maps to something outside of $B$, we take that $n$ and map it to $z$. And more importantly, everything else, we refer to $g$ on how to map things. Since $g$ is surjective on $B$, anything in $B\setminus A$ is “redirected” to $z\in A$. Meanwhile all the other stuff in $A$ is given as-is.

1. Let $B$ be countably infinite, and $A$ be a subset of $B$. If $A$ is empty, we are done, since $A$ is finite, therefore countable.
2. Therefore we now assume $A$ is non-empty.
3. Since we know $A$ is non-empty, $\exists z\in A$.
4. By line 1, we know that there exists a bijection $f:\mathbb{N}\to B$.
5. Now create function $g:\mathbb{N}\to A$, where:

$$g:n\mapsto \{\begin{array}{ll}z& ,\text{ if }f(n)\in B\setminus A\\ f(n)& ,\text{ otherwise}\end{array}$$

6. Note that $g$ only maps to elements in $A$, since $f$ maps to $B\setminus A$ or $A$, and when it does map to $B\setminus A$, $g$ maps to $z\in A$.
7. Now let $a\in A$, arbitrarily chosen.
8. Since $f$ was surjective on $B$, and $a\in B$ (because $A\subseteq B$), $\exists i\in \mathbb{N}$ such that $f(i)=a$.
9. Since $f(i)\notin B\setminus A$, $g(i)=f(i)=a$.
10. Therefore $\forall a\in A,\exists i\in \mathbb{N}[g(i)=a]$.
11. Therefore $g:\mathbb{N}\to A$ is a surjection.
12. Thus, $A$ is countable.

Let $A,B$ sets (not necessarily disjoint). Let $A$ be countably infinite, and $B$ be finite. Then $A\cup B$ is countably infinite.

Idea:

1. Consider $C=A\cap B$. Since $C\subseteq B$, $C$ is finite. (Subset of finite set is finite.)
2. Therefore there exists $k\in \mathbb{N}$ and bijective function such that $f:{\mathbb{Z}}_k$.
3. Define sets $E=A\setminus C$, and $D=B\setminus C$.
4. Now $C,D,E$ are disjoint. (Why?)
5. Furthermore, $C,D$ are finite, and $E$ is countably infinite.

Your turn: At this point, at line 5, can we somehow use our previous ideas to argue that there exists a bijection function $g:{\mathbb{Z}}^{+}\to C\cup D\cup E$? Can we also argue that $C\cup D\cup E=A\cup B$?

Let $A,B$ be sets, (not necessarily disjoint). Let $A$ and $B$ both be countably infinite. Then $A\cup B$ is countably infinite.

We want to do the same idea, let’s try repeating the idea as before: We want to take $C=A\cap B$ and try to list out the elements in $C$, and also $A\setminus C$, and $B\setminus C$.

1. Let $A,B$ be sets, and countably infinite. Consider $C=A\cap B$.
2. Since $C\subseteq A$, $C$ is countable. (By the lemma)
3. Let $D=A\setminus C$, and $E=B\setminus C$. Both $D,E$ are countably infinite. (By the lemma)
4. By definition of countability, $C$ is either finite or countably infinite.
5. Case 1: $C$ is finite.
   1. In this case, we know that $C,D,E$ are disjoint, and $C$ is finite, $D,E$ are countably infinite.
   2. Your turn: Using the statements above, what should we do in order to give a bijection $g:{\mathbb{Z}}^{+}\to C\cup D\cup E$?
   3. How do we argue that $C\cup D\cup E=A\cup B$?
6. Case 2: $C$ is countably finite.
   1. In this case, we know that $C,D,E$ are disjoint, and $C,D,E$ are countably infinite.
   2. Your turn: Using the statements above, what should we do in order to give a bijection $g:{\mathbb{Z}}^{+}\to C\cup D\cup E$?
   3. How do we argue that $C\cup D\cup E=A\cup B$?

If $A,B$ are countably infinite sets, then $|A\times B|={\aleph }_0$

Let $A,B$ be countably infinite. Then there exists bijections $f:\mathbb{N}\to A$, and $g:\mathbb{N}\to B$ such that $f,g$ bijective.

For $|A\times B|$, it suffices to show that $|A\times B|=|\mathbb{N}\times \mathbb{N}|$, since we know the latter has a bijection to $|\mathbb{N}|$.

Consider $h:\mathbb{N}\times \mathbb{N}\to A\times B$, where $h(i,j)\mapsto (f(i),g(j))$. We know that since $f(i)\in A,g(j)\in B$, $h(i,j)\in A\times B$.

1. Let $(a,b)\in A\times B$, arbitrarily chosen.
2. Now since $f$ is surjective, exists $i\in \mathbb{N}$ such that $f(i)=a$.
3. Now since $g$ is surjective, exists $j\in \mathbb{N}$ such that $g(j)=b$.
4. Therefore $h(i,j)=(f(i),g(j))=(a,b)$.
5. By universal generalisation $\forall (a,b)\in A\times B,\exists i,j\in \mathbb{N}[h(i,j)=(a,b)]$.

What if we changed the above statement to either $A$ or $B$ being finite?

If $A$ is countably infinite, and $B$ is finite then $|A\times B|={\aleph }_0$

Now this one, one intuition is the following: we can create a function that basically just lists out all elements of $A$, but if $B$ is for example, size $3$, then we basically first list $(a_0,b_1),(a_0,b_2),(a_0,b_3)$, then list $(a_1,b_1),(a_1,b_2),(a_1,b_3)$, and so on. So we want to map $0$ to $(0,1)$, $1$ should map to $(0,2)$, $2$ should map to $(0,3)$, $4$ should map to $(1,1)$ and so on. So a number $n$ should map to $(k,i)$ where $n=t\cdot k+(i-1)$, where $t$ is the size of $b$, and $i$ ranges from $1$ to $k$.

1. Assume $A$ is countably infinite, and $B$ be finite.
2. Therefore exists $f_A:\mathbb{N}\to A$ that is a bijection.
3. Also exists $k\in \mathbb{N}$, $f_B:{\mathbb{Z}}_k\to B$ that is a bijection.
4. Consider function $g:\mathbb{N}\to (A\times B)$, where $g:n\mapsto (f_A(t),f_B(i)),\text{ where }\exists t\in \mathbb{N},i\in {\mathbb{Z}}_k[n=k\cdot t+(i-1)]$

Remarks: To be clear, there’s the $i-1$ because $i$ ranges from $1$ to $k$.

To summarise, I think knowing these facts hopefully give you an intuition on what is countable. For example, $\mathbb{Z}$ is pretty much just “two copies” of $\mathbb{N}$ (but only one $0$). So it’s almost “two natural sets”. In fact, instead of using a bijection, let’s try using a surjection to show that. And maybe you’ll see how surjections are a lot easier to use. So let’s prove this:

$\mathbb{Z}$ is countably infinite.

We’ll basically be giving a surjection from $\mathbb{N}\times \{0,1\}\to \mathbb{Z}$. Why? Because we can re-use the previous parts to argue that $\mathbb{N}\times \{0,1\}$ has a bijection from $\mathbb{N}$. So we can compose those functions to get $\mathbb{N}\times \{0,1\}\to \mathbb{Z}$ which is surjective but not injective.

Again, we’ll just give the surjection.

1. Consider function $g:\mathbb{N}\times \{0,1\}\to \mathbb{Z}$.
2. Define $g:(n,s)\mapsto \{\begin{array}{ll}n,& \text{ if }s=0\\ -n,& \text{ if }s=1\end{array}$

To prove it’s surjective intuitively, every value is output at least once. Any positive output $x$ is mapped to by $(x,0)$, and $-x$ is mapped to by $(x,1)$. But why is it not injective?

Now the surjection is not enough. That only proves it’s countable. But I mean we all know that $\mathbb{Z}$ is infinite so we’ll just say it’s countably infinite. (We could prove it but please don’t make me prove it. Please.)

Using “countably infinite” and bijection to $\mathbb{N}$ interchangeably.

So to be clear, you’re going to see it quite often that when we say a set $A$ is countably infinite, then the following are synonymous:

1. $|A|={\aleph }_0$
2. $|A|=|\mathbb{N}|$
3. $|A|=|{\mathbb{Z}}^{+}|$

That’s why you’ll see us sometimes use bijection $f:\mathbb{N}\to A$ when convenient, and other times using bijection $g:{\mathbb{Z}}^{+}\to A$ instead.

But why? Is there a reason for this? Is $\mathbb{N}$ and ${\mathbb{Z}}^{+}$ special?

Technically not, if you know there are two sets $A,B$ both countably infinite, then of course you now have $f_A:\mathbb{N}\to A$ and $f_B:\mathbb{N}\to B$. They’re both bijections, so now you can do consider $f_B\circ f_A^{-1}:A\to B$. We know $f_A^{-1}$ is a bijection also, and the composition of two bijections forms a bijection so now $f_B\circ f_A^{-1}:A\to B$ is a bijection between the two of them. After all they’re both countably infinite, this means they have the same cardinality, so you should be able to find a bijection between them.

The “nice” thing about bijections $f:\mathbb{N}\to A$ and $g:{\mathbb{Z}}^{+}\to A$ is that they tell you how to list out the elements in some kind of sequence. To be very clear: that sequence will and must list out all elements of $A$.

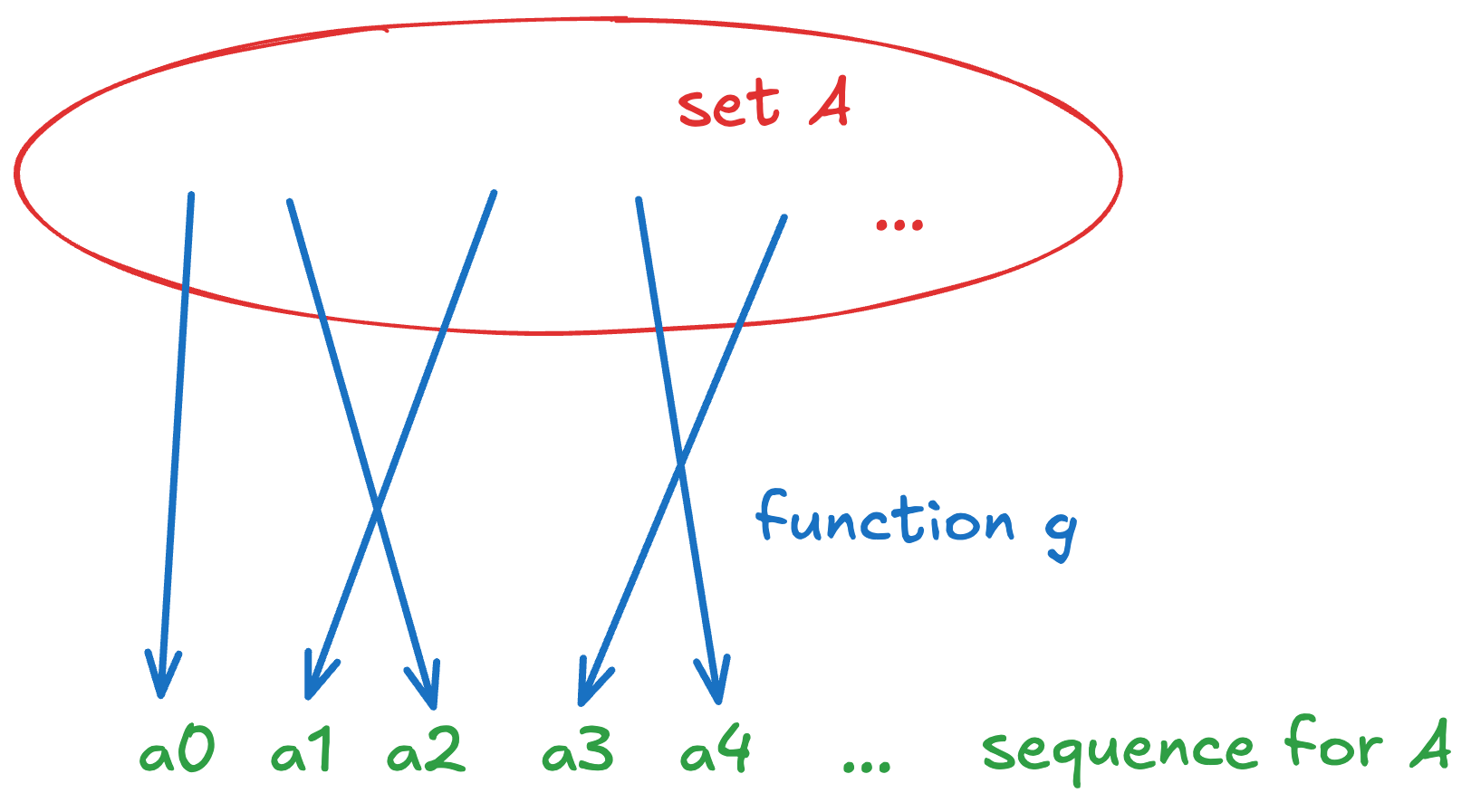
The idea is that if you fail to do so, then the set is uncountably infinite.

Moving out of Countably Infinite

Okay, is there more than one “infinite size”? After all, countably infinite implies existence of uncountably infinite amirite?

So what’s the best candidate we have for an uncountably infinite set? The set of reals $\mathbb{R}$. After all, think about it: Can we construct a bijection from $\mathbb{N}$ to $\mathbb{R}$? We’re going to show that if one exists, we can create a contradiction.

Now to be clear, if we show that there is no bijection, we are only showing $|\mathbb{N}|\ne |\mathbb{R}|$. Intuitively, we also want to show that $|\mathbb{N}|\le |\mathbb{R}|$. To do this, we can just give some injective function $f:\mathbb{N}\to \mathbb{R}$. But that’s easy! $f:n\mapsto n$. Et Voila. Let’s move onto showing there’s no bijection.

Cantor’s Diagonalisation Argument

We’ll actually use ${\mathbb{Z}}^{+}$, but we know that $|{\mathbb{Z}}^{+}|=|\mathbb{N}|$.

Aside

I don’t know if they told you this but you’re about to see diagonalisation in a bit. And this is one of the most powerful techniques in math and CS combined. Some of the biggest and most famous theorems about logic, the naturals vs the reals, about the nature of computation, about computational complexity theory, all use diagonalisation.

I’ll show you how to do it for the reals, then also show you how to do it for computation. But that one will be extra handwavy.

Let $I$ be the set $\{x\in \mathbb{R}:0<x\wedge x<1\}$ or just $(0,1)$.

We will show the two following claims:

Claim 1: There exists an injective function $f:{\mathbb{Z}}^{+}\to I$. Therefore $|{\mathbb{Z}}^{+}|\le |I|$ Claim 2: There exists no bijection function $g:\mathbb{N}\to I$. Therefore $|{\mathbb{Z}}^{+}|\ne |I|$ Claim 3: There exists an injective function $h:I\to \mathbb{R}$. Therefore $|I|\le |\mathbb{R}|$

Using all 3 claims, we get that:

$$|{\mathbb{Z}}^{+}|⪇|I|\le |\mathbb{R}|$$

(We actually haven’t shown $\le$ on set cardinalities are transitive. Perhaps that’s a good exercise. We need to show it’s transitive to show that claims 1-3 imply $|{\mathbb{Z}}^{+}|⪇|\mathbb{R}|$.)

Claims 1 and 3 are actually somewhat straightforward. We’ll give the functions here, and it’ll be a mini-exercise to prove they are injective, and that their co-domains are correct.

$$\begin{array}{rl}& f:x\mapsto \frac{1}{x+1}\\ & h:x\mapsto x\end{array}$$

We need the fact that every $x\in I$ has a “decimal expansion”.

Lemma: For all $x\in \mathbb{R}$ such that $0\le x\wedge x<1$, there exists a function $d:{\mathbb{Z}}^{+}\to \{0,1,2,3,4,5,6,7,8,9\}$ such that, letting $x_i=d(i)$, then $x=x_1{x}_2{x}_3\dots$ Or equivalently:$x={\sum }_{i\in {\mathbb{Z}}^{+}}d(i)\times 10^{-i}$ For $x\in I$, let $d_x$ be the function for $x$. In other words, given a real value $x$, $d_x$ is what we use to list out the decimal points.

To prove the above lemma is pretty annoying unless you have a background in Real Analysis. So we’ll just take this as fact (I’m sure we can all believe it). Here’s the strategy:

1. We want to assume that a bijection $g:{\mathbb{Z}}^{+}\to I$ exists. Remember this means $g$ will list out all elements in $I$ somehow (surjection, injection).
2. We will use $g$ to create another element $y$ so that $y\in I$, but $y$ is somehow not a possible output of $g:{\mathbb{Z}}^{+}\to I$.
3. That’s a contradiction because $g$ was supposed to be bijective, and therefore surjective. But line 2 shows that $g$ is not surjective.

Remember, this means that $g:{\mathbb{Z}}^{+}\to I$ on a positive integer $n$ gives us a value $x$ from set $I$. Furthermore, any value $x$ in $I$ can be written in decimal representation using function $d_x$. In particular, the $d_x(j)$ gives us the $j^{th}$ decimal place of $x$.

So how do we create the value $y$? We’ll build it decimal place by decimal place. The $i^{th}$ decimal place of $y$, will be done based on $i^{th}$ decimal place of the $i^{th}$ output of $g:{\mathbb{Z}}^{+}\to I$. Yes, that is not a typo: We take the $i^{th}$ number, and look at its $i^{th}$ decimal place. Then what do we do? If that decimal place happens to be $1$, we set the $i^{th}$ decimal place of $y$ to be $2$. If that decimal place happens to be anything but $1$, we’ll set the $i^{th}$ decimal place of $y$ to be $1$. Why does this work?

Let’s ask ourselves: $y$ is definitely a number in the interval $(0,1)=I$ so it has to be output by $g:{\mathbb{Z}}^{+}\to I$, since it was assumed to be bijective (and therefore surjective).

Okay, so here comes the kicker: What is the $z^{th}$ decimal place of $y$? Remember, to set it, we said we looked at the $z^{th}$ output of $g:{\mathbb{Z}}^{+}\to I$ and we purposely set the $z^{th}$ decimal place of $y$ so that it would be different from it.

But wait! That means $g(z)\ne y$ (because they disagree on the $z^{th}$ decimal point). Since we let $z$ be arbitrarily chosen, that means $\forall z\in {\mathbb{Z}}^{+}[g(z)\ne y]$. Oh no! That means $g$ is not surjective. But how can that be! It was supposed to be bijective (and therefore surjective).

Here’s the idea in proof form.

Proof by contradiction.

1. Assume for a contradiction that there exists a bijection $g:{\mathbb{Z}}^{+}\to I$.

2. For all $i\in {\mathbb{Z}}^{+}$, $g(i)\in I$, therefore $d_{g(i)}$ exists.

3. Now define a new function $d_y:{\mathbb{Z}}^{+}\to \{0,1,2,3,4,5,6,7,8,9\}$ in the following way:

   $d_y(i)=\{\begin{array}{ll}1& \text{ if }{d}_{g(i)}(i)\ne 1\\ 2& \text{ if }{d}_{g(i)}(i)=1\end{array}$

   Thus, let $y={\sum }_{i\in {\mathbb{Z}}^{+}}{d}_y(i)\times 10^{-i}$.

4. Now notice, by definition of $d_y$:

   1. Let $i\in {\mathbb{Z}}^{+}$, arbitrarily chosen.
   2. $d_y(i)\ne d_{g(i)}(i)$.
   3. Since $y$ and $g(i)$ differ on the $i^{th}$ decimal place, $y\ne g(i)$.
   4. Therefore, by universal generalisation $\forall i\in {\mathbb{Z}}^{+}[y\ne g(i)]$.

5. By line $4$, this means $y$ is not in the range of $g(i)$.

6. But note that $y<1$ and $y>0$. Since $y$ only has decimal places that are either $1$ or $2$.

7. Therefore $y\in I$. But this means that $g$ is not a surjection on $I$.

8. Line 7 contradicts line 1. Therefore there does not exist bijections from ${\mathbb{Z}}^{+}\to I$.

This proof is basically an informal version of Cantor’s Diagonalisation Argument.

I’ll drawn some diagrams that might help explain the idea:

Diagrammatically:

The idea is that any number between 0 and 1 and can be written out in the following way:

Where all of the $d(j{)}_{g(i)}$ happens to be a number between 0 and 9. So in particular:

$$g(i)=\sum _{j\in {\mathbb{Z}}^{+}}10^{-j}d(j{)}_{g(i)}$$

So what happens if we took every number on the diagonal and collected them. Then did a bunch of changing? Like so:

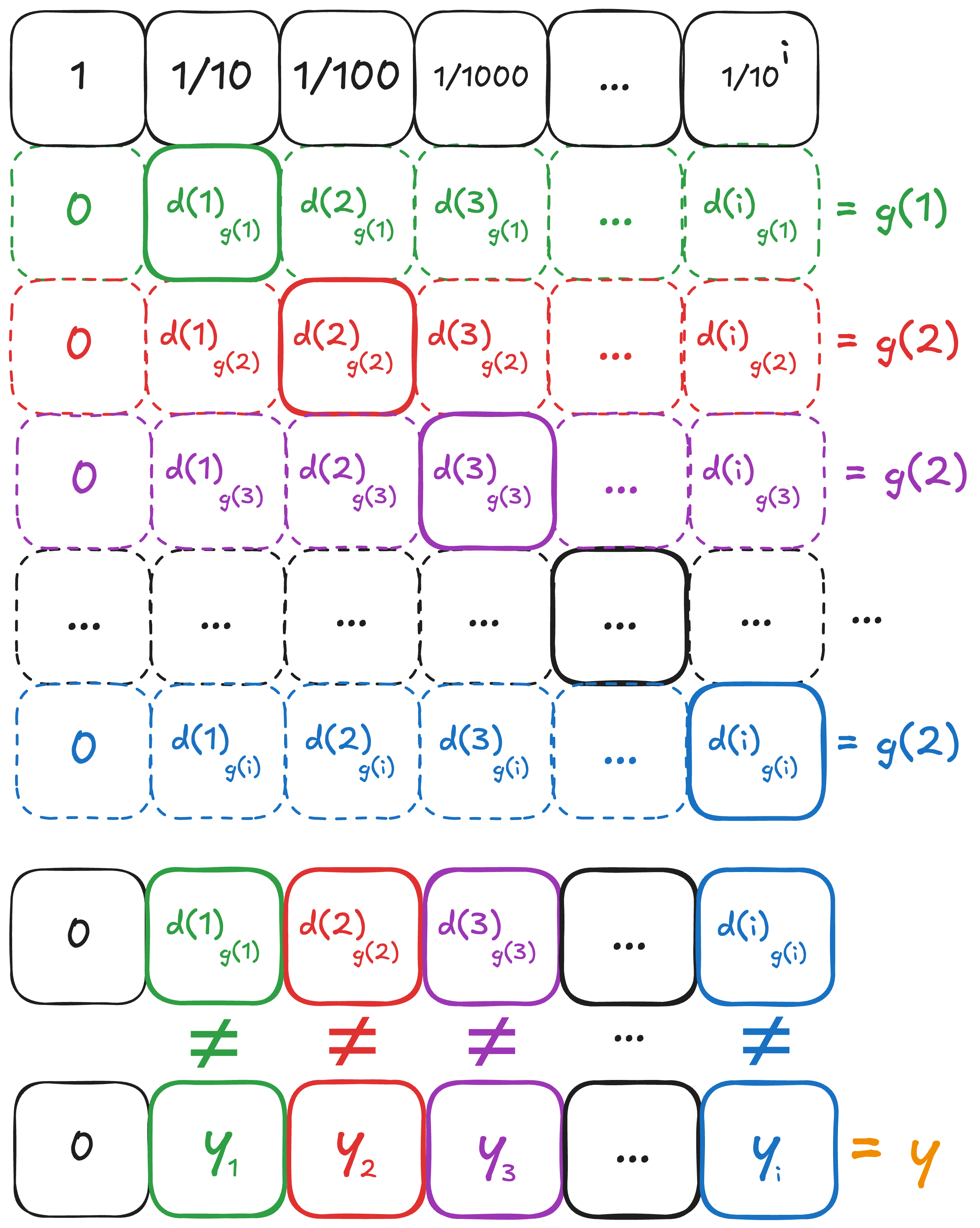
As long as we make all the $y_i$ values a value between 1 and 8 (inclusive) then

$$y=\sum _{i\in {\mathbb{Z}}^{+}}{y}_i\times 10^{-i}$$

is a value greater than $0$, and strictly less 1. The bigger question is whether $y$ can be an output of $g$. Well we claim the answer is no. Why? Look at the $i^{th}$ output of $g$. That happens to be $g(i)$. Then look at the $i^{th}$ decimal place of $g(i)$, that happens to be $d(i{)}_{g(i)}=g(i{)}_i$. Now we made the $i^{th}$ decimal place of $y$ (which is $y_i$) different from $d(i{)}_{g(i)}=g(i{)}_i$ . So that means $y$ cannot be equals to $g(i)$ (since they differ on the $i^{th}$ decimal point). So the above formal proof is basically just carrying that idea out.

But to be clear, $\mathbb{R}$ is infinite, and it’s uncountable. So therefore, it is uncountably infinite.

Another generic way to create uncountable sets

There’s another way you can do this:

Theorem

Let $A$ be countably infinite. Then $\mathcal{P}(A)$ is uncountably infinite.

So the idea is to show two things: $\mathcal{P}(A)$ is infinite, we can do that with a simple function $f:A\to \mathcal{P}(A)$, where $f:a\mapsto \{a\}$. This function is injective, and $A$ is infinite, so $|A|\le |\mathcal{P}(A)|$.

Now we need to show there is no bijection. So here’s what I’m going to do. I’ll draw the diagonalisation diagram. But you need to write out the proof formally. Okay here goes:

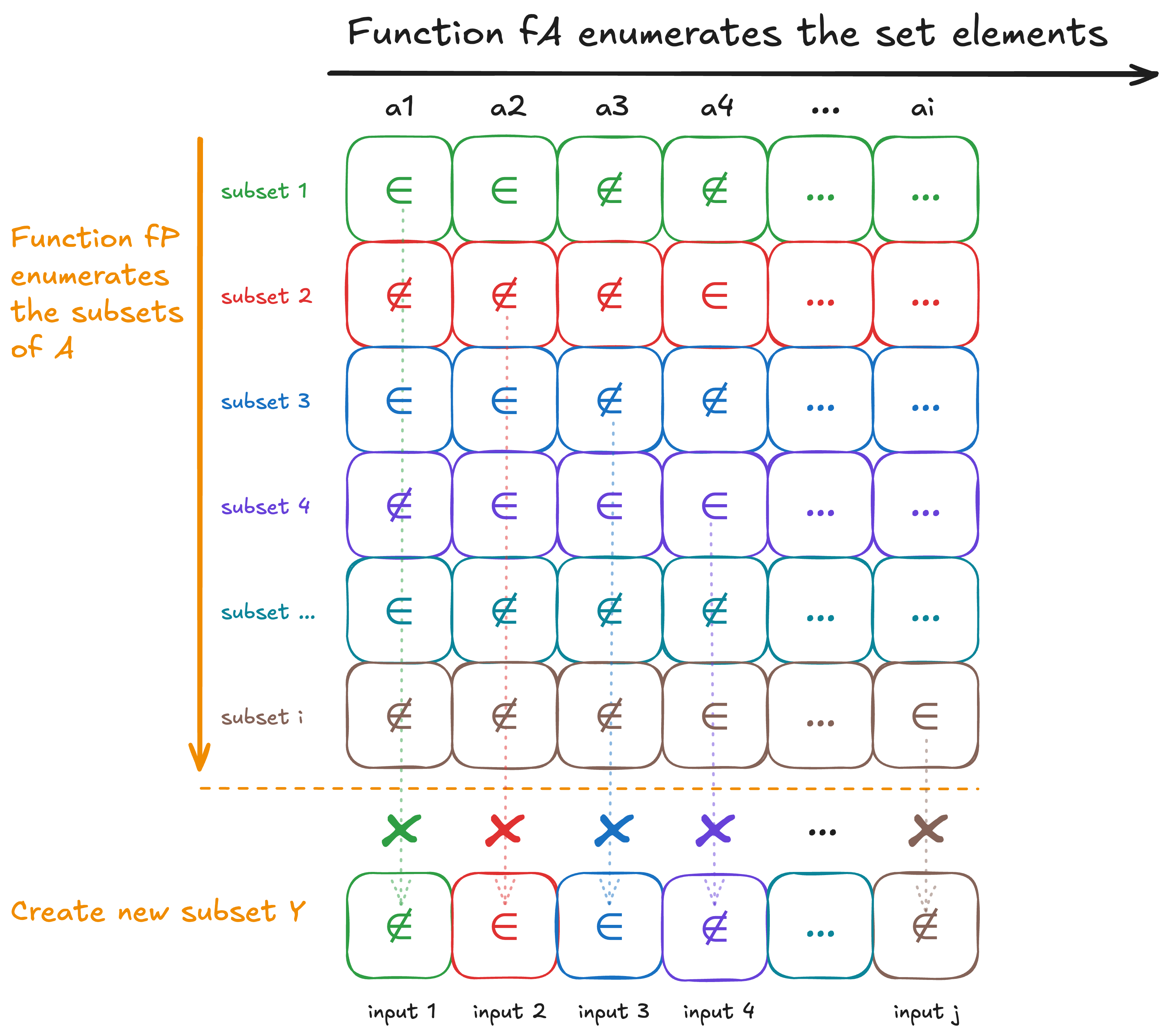
For you to write your proof, what should you assume for the sake of contradiction? How should you create set $Y$? What two properties do you want about $Y$ to derive a contradiction?

Once you are done with this, since $Y$ is infinite, $Y$ has no bijection to a countable set, therefore $Y$ is uncountably infinite.

Aside

So have we created the next cardinality after ${\aleph }_0$?

Well.. that’s complicated. We know that the reals indeed has a cardinality larger than the naturals. It turns out we actually cannot prove whether or not $|\mathbb{R}|={\aleph }_1$. Like not that humans are not smart enough. No, more like the proof system we all use is unable to. At least not with the current axioms we like to take for granted.

Tl;dr: The next cardinality after ${\aleph }_0$ happens to be ${\aleph }_1$, but we cannot prove whether $\mathbb{R}$ has cardinality ${\aleph }_1$ or not.

Working with Uncountable Infinity

Now working with uncountable infinity is a lot more wacky. We’ll try to build our way up to at least prove the following theorem at the end of this section:

Theorem

Let $B$ be an uncountably infinite set and $C$ be a finite set. Explicitly give a bijection $f:B\cup C\to B$.

In the meantime, let’s prove some useful theorems about uncountable sets.

Theorem

Let $B$ be uncountably infinite, and let $C$ be finite. Then $B\setminus C$ is uncountably infinite.

Here’s the idea, if $B\setminus C$ is not uncountably infinite, then $B\setminus C$ must be countable. In both cases, we show that it is pretty absurd.

Proof

1. Let $B$ be uncountably infinite. Let $C$ be finite.
2. Consider $B\setminus C=E$.
3. Assume for the sake of a contradiction that $E$ countable.
4. Then, either $E$ is finite, or uncountably infinite.
5. Case 1: $E$ is finite.
6. Then $E\cup C$ is finite. (Union of the two finite sets is finite.)
7. But then $B=E\cup C$ is finite.
8. But $B$ is uncountably infinite.
9. Contradiction.
10. Case 2: $E$ is countably infinite.
11. Then $E\cup C$ is countably infinite. (By previous part)
12. But $B=E\cup C$ is countably infinite.
13. But $B$ is uncountably infinite.
14. Contradiction.
15. In both cases we’ve obtained a contradiction. Therefore $E$ is uncountable.

You can try doing something similar when $C$ is countably infinite. Give is a try and see what changes compared to the current proof.

Here’s another idea, if $B\subseteq D$, and $B$ is uncountably infinite. Then $D$ is uncountably infinite. So there are a few ways to prove this. But here’s the idea, in CS1231S I think they’ve bottomed-out the formalism and end at just saying “Look a set is either finite, countably infinite, or uncountably infinite.” If you can believe that countably infinite happens to be the smallest “infinite” size, and you also can believe that $|A|\le |B|$ if and only if $f:A\to B$, then this means that any infinitely sized set $C$ is at least as large as $\mathbb{N}$. That is to say, you now have an injection $f:\mathbb{N}\to C$. You can take this injection, and ask: What is the range of $f$? Not the co-domain, that happens to be $C$. The range is exactly the set of elements that $f$ maps to. This set is countable! In fact, $f$ is precisely a bijection from $\mathbb{N}$ to its output set — the range of $f$.

Now also, the range of $f$ happens to be a subset of $C$. So, if we know that $C$ is infinitely sized, then we know that there must exist a countable subset of $C$. This just somewhat follows from our intuition that $\mathbb{N}$ is the smallest possible infinitely sized set.

Can we actually prove it? So what I gave you was a sketch. I used the fact that:

1. $\mathbb{N}$ is the smallest possible infinitely sized set.
2. Therefore, $|\mathbb{N}|\le |C|$, since $C$ is infinitely sized.
3. Therefore, exists injective function $f:\mathbb{N}\to C$.
4. Then consider the range of $f$, i.e. $ran(f)=\{f(n):n\in \mathbb{N}\}$.
5. $f$ is also a bijection $f:\mathbb{N}\to ran(f)$.
6. Also, $ran(f)\subseteq C$, since $f:\mathbb{N}\to C$.
7. Therefore $ran(f)$ is a countably infinite subset of $C$.

We could be more formal than this, but not in CS1231S.

Also we can also say the following:

Theorem

If there exists sets $B,D$, such that $B\subseteq D$ and $B$ is uncountably infinite, then $D$ is uncountably infinite.

This follows from the fact that if $D$ is countable, then any subset of $D$ is either finite, or uncountably infinite.

Theorem

Let $B$ be a finite set. Then if $C$ is a set such that $C\subseteq B$, then $C$ is also finite. Let $D$ be countably infinite. Then if $E$ is a set such that $E\subseteq D$, then $E$ is countable.

Okay! Let’s try proving the theorem we started the subsection with. Restating it here:

Theorem

Let $B$ be an uncountably infinite set and $C$ be a finite set. Explicitly give a bijection $f:B\cup C\to B$.

Proof

1. Let $B,C$ be sets such that $C$ is finite, and $B$ is uncountably infinite.
2. Now consider $E=C\setminus B$.
3. Since $E\subseteq C$, and $C$ is finite, $E$ is also finite.
4. Furthermore, since $B$ is infinite, exists $B^{\prime }$ that is a countably infinite subset of $B$.
5. Since $B^{\prime }$ is countably infinite, we have a bijection $f:{\mathbb{Z}}^{+}\to B^{\prime }$.
6. Since $E$ finite, and $B^{\prime }$ countably infinite, then $E\cup B^{\prime }$ is countably infinite. (We proved this earlier on a few sections ago.)
7. So this means that there exists a bijection function $g:{\mathbb{Z}}^{\to }{B}^{\prime }\cup E$.
8. Composing $f\circ g^{-1}$, we get a bijection $g^{\prime }:B^{\prime }\cup E\to B^{\prime }$.
9. Furthermore, note that $E$ and $B$ are disjoint. (Since $E=C\setminus B$).
10. So now define our bijection $h:x\mapsto \{\begin{array}{ll}x& ,\text{ if }x\notin (B^{\prime }\cup E)\\ g^{\prime }(x)& ,\text{ if }x\in (B^{\prime }\cup E)\end{array}$

So what’s the idea? What is it trying to do? Here’s a picture:

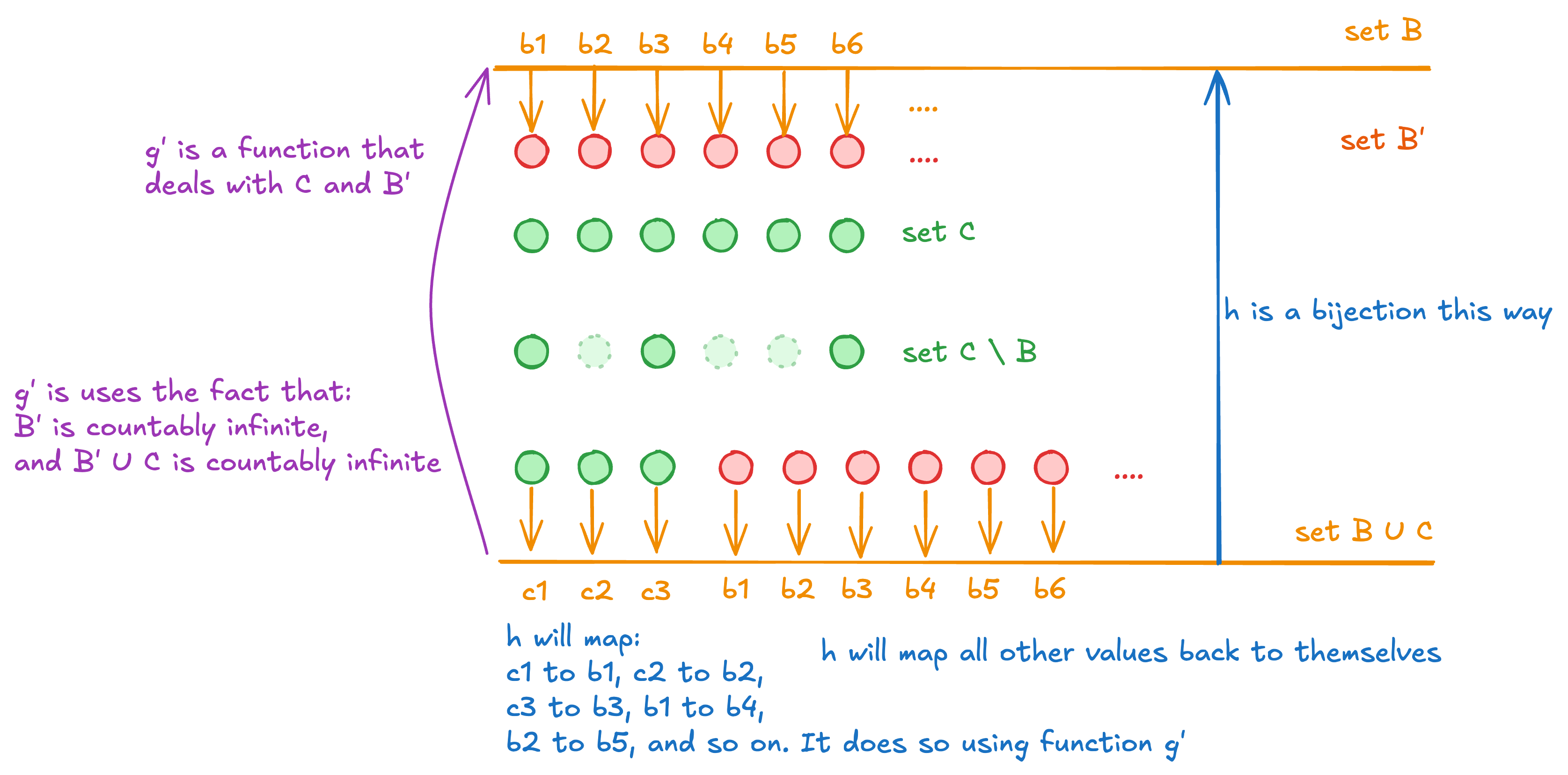
Here’s the idea: We take set $C$ and remove the elements already in $B$. In my picture let’s say that means $3$ elements remain. Also, we take set $B^{\prime }$ which I stress: is countably infinite from set $B$. Then we re-use the idea that we can union a countably infinite set with a finite one to get a countably infinite set.

Now we need to “slot it back it”. In some sense, we’ve shifted the $b_1,b_2,\dots$ over to the right by $3$ positions in the diagram. We’ve made holes in the original set $B$ that can now be mapped to $c_1,c_2,c_3$.

So to create the function $h$ as a bijection, the idea is: On input $x\in B$, you ask yourself: is $x\in B^{\prime }\cup C$? Because if it is, we can use the $g^{\prime }$ function to ask what was the original value. Otherwise, $x\notin B^{\prime }\cup C$, in which case you should just forward the value along. It wasn’t involved in being shifted around.

How is this relevant to computer science?

So this proof idea actually extends to computer programs and program analysis. (Also further beyond that). I have two theorems to offer you, both saying roughly the same thing. Also I will only make informal statements because to formalise these concepts, you’ll need a full semester so the notions here are only pseudo-formal but should convey the key idea nonetheless.

Claim 1: There exist unsolve-able problems by computer programs.

Claim 2: Let $\mathcal{D}:\mathbb{P}\times \mathbb{I}\to \{true,false\}$ be the following problem: Let $\mathbb{P}$ be the set of computer programs, let $\mathbb{I}$ be the set of program inputs. Let $P\in \mathbb{P}$ be a computer program, let $I\in \mathbb{I}$ be a program input. Then $\mathcal{D}:(P,I)\mapsto true$, if program $P$ on input $I$ will terminate. Otherwise, $\mathcal{D}$ outputs $false$.

Let’s begin with the first one. We first need a simple formalisation of a computer program. To simplify things, let’s consider problems as functions $Q:\mathbb{I}\to \{yes,no\}$. So $Q$ is a problem, because it takes a program input, and $Q$ specifies for each input whether you need to say yes, or no. Here’s an example:

Example

Is Sorted Problem: Let $\mathbb{I}$ be the set of all lists of numbers. Then $Q:\ell \mapsto true$ if and only if the list $\ell$ is sorted. $Q$ outputs $false$ otherwise.

Bear in mind, $Q$ is not a program, it’s a problem. That means to solve the sorted problem, you need to give a computer program $P$, maybe in Source, or in Javascript or Python, such that for all inputs $\ell \in \mathbb{I}$, $P(\ell )=Q(\ell )$. Why are they different? Because you can write many programs that solve the same problem. After all, I’m sure you’ve seen at least your classmates write different code to solve the same problem. Here’s another example:

Example

Is Palindromic Problem: Let $\mathbb{I}$ be the set of all strings. Then $Q:s\mapsto true$ if and only if $s$ is a palindromic string.

Okay, so here’s a few observations we need to make in our formalisation. We think of our input as finite length objects. Our input lists or strings should be finite in length. And furthermore, there are countably infinitely many of such inputs. This means that our $\mathbb{I}$ is basically a countably infinite set.

I already hear the 1% of you protesting: “But what about infinite lists as our input or uncountably infinitely sized input sets $\mathbb{I}$?“. Well do you want your program to take forever to just read the inputs? Also uncountably large $\mathbb{I}$ is technically not an issue, but let’s table that for another day.

Okay, now you know what a problem $Q:\mathbb{I}\to \{true,false\}$ is. I’ll tell you up front, if $\mathbb{I}$ is countably infinite, then $Q$ as a set is also countably infinite. I won’t prove this here because it’s beside the point.

Let $\mathcal{Q}$ be the set of all problems $\{Q\subseteq (\mathbb{I}\times \{true,false\}):Q\text{ is a function }\mathbb{I}\to \{true,false\}\}$. Yes we can formalise set using first order logic, but I’ll skip that, we’re doing big picture right now.

Now, what is the cardinality of $\mathcal{Q}$? I’m actually going to show you that $|[0,1]|\le |\mathcal{Q}|$. How do we do this? Here’s the trick: We will construct an injection $c:[0,1]\to \mathcal{Q}$. And we know this interval itself has cardinality strictly larger than any countably infinite set. Thanks Dr. Georg Cantor.

The overall idea is the following:

1. Take $x\in [0,1]$.
2. Write $x$ out in binary expansion as ${\sum }_{i\in {\mathbb{Z}}^{+}}{x}_i\cdot 2^{-i}$, where $x_j\in \{0,1\}$, for all $i\in {\mathbb{Z}}^{+}$.
3. Then when $x_i$ is $1$, we map it to $true$, and $x_i$ is $0$, we map it to $false$.
4. Then this sequence of $true$ and $false$ defines a problem $Q$.
5. The last thing to do is to map the sequence back into $\mathbb{I}$.

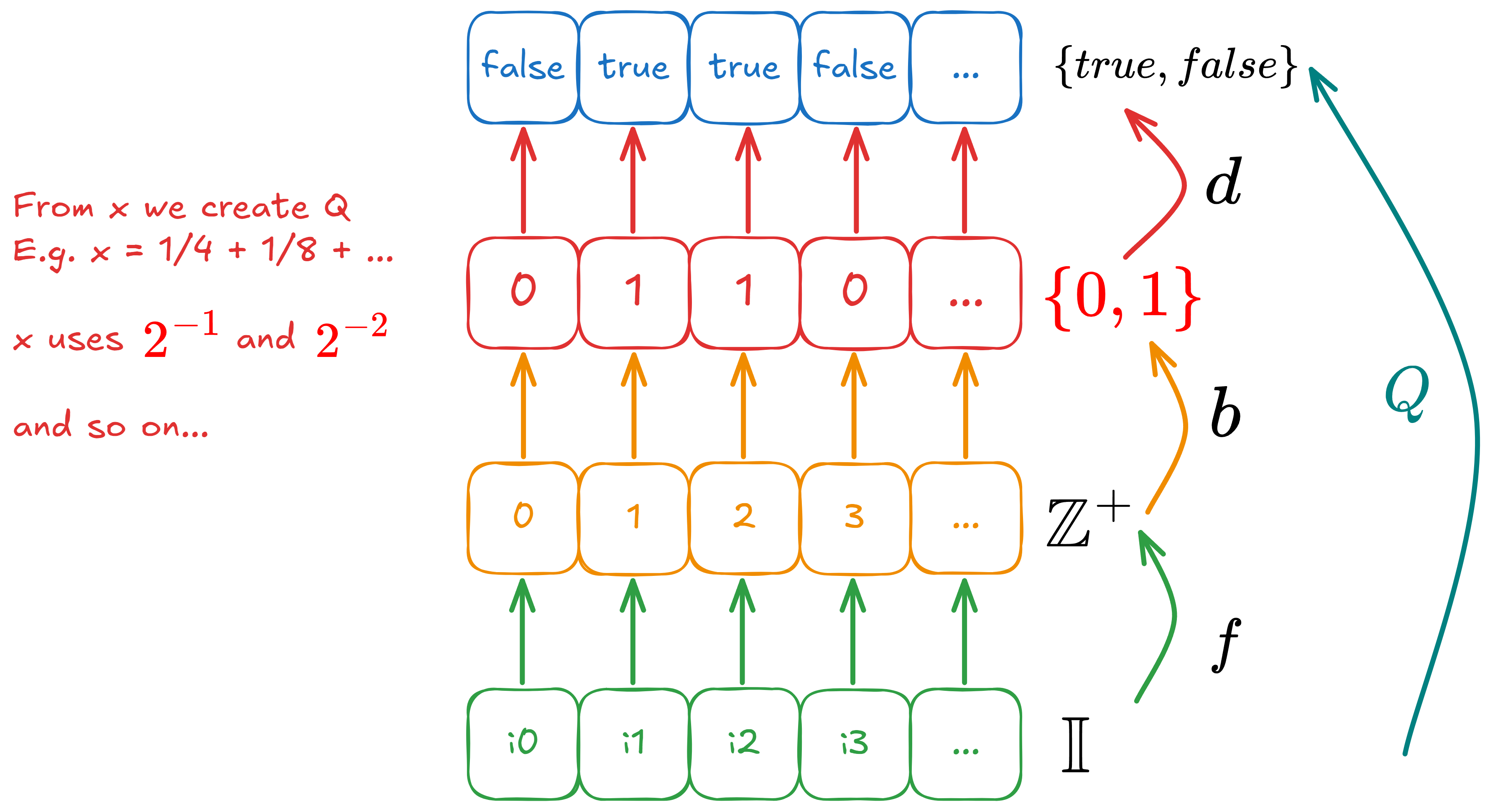
Pseudo-formally: We want to create a mapping $c:[0,1]\to Q$ where $c$ is injective.

1. Since $\mathbb{I}$ is a countably infinite set, there exists a bijective function $f:{\mathbb{Z}}^{+}\to \mathbb{I}$.
2. Let $x\in [0,1]$. Then $x$ can be written as ${\sum }_{i\in {\mathbb{Z}}^{+}}{x}_i\cdot 2^{-i}$, where $x_i\in \{0,1\}$, for all $i\in {\mathbb{Z}}^{+}$.
   1. Alternatively, one can say there is a corresponding function $b:{\mathbb{Z}}^{+}\to \{0,1\}$ for which $x={\sum }_{i=1}^{\infty }b(i)\cdot 2^{-i}$.
3. Create a mapping $d:{\mathbb{Z}}^{+}\to \{true,false\}$, where:
   1. $d(i)=true$ if $x_i=1$;
   2. $d(i)=false$ if $x_i=0$
   3. Note: $d$ is a bijection.
4. Since $|{\mathbb{Z}}^{+}|=|\mathbb{Z}|=|\mathbb{I}|$, exists a bijective function $f:\mathbb{I}\to {\mathbb{Z}}^{+}$.
5. We now move to create a problem $Q$. This means $Q$ has to be a function from $\mathbb{I}\to \{true,false\}$.
   1. On input $I\in \mathbb{I}$, note that since $f$ is a function, $f$ maps $I$ to a unique value $n\in {\mathbb{Z}}^{+}$.
   2. Since $f:\mathbb{I}\to {\mathbb{Z}}^{+}$, $b:{\mathbb{Z}}^{+}\to \{0,1\}$, $d:\{0,1\}\to \{true,false\}$ are functions, then:
   3. $(d\circ b\circ f):\mathbb{I}\to \{true,false\}$ is a well-defined function.
   4. Define $Q=(d\circ b\circ f)$. Note, the choice of $b$ depends on $x$. The choice of $f$ and $d$ are fixed beforehand. Furthermore, $f$ and $d$ are bijections.
6. Then $Q$ is a function $\mathbb{I}\to \{true,false\}$.
7. Thus, for an arbitrary $x\in [0,1]$, we have constructed a function $Q_x$. Thus by universal generalisation, $\forall x\in [0,1]$, $\exists Q[Q:\mathbb{I}\to \{true,false\}]$. In other words, on any input $x$, there exists an output $Q$.
8. Furthermore, let $x_1,x_2\in [0,1]$ be arbitrarily chosen such that $Q_1$ was created (using lines 1-5) using $x_1$, and $Q_2$ was created using $x_2$. And further assume $Q_1\ne Q_2$.
9. Then, there exists $I\in \mathbb{I}$ such that $Q_1(I)\ne Q_2(I)$. (They differ when given input $I$.)
10. Since $Q_1(I)=d(b_1(f(I)))$ and $Q_2(I)=d(b_2(f(I)))$, and $d$ is a bijection:
11. $Q_1(I)\ne Q_2(I)$ imply that $d(b_1(f(I)))\ne d(b_2(f(I)))$.
12. And because $d$ is a bijection, $b_1(f(I))\ne b_2(f(I))$.
13. Therefore $x_1$ and $x_2$ differ in their binary representation at location $f(I)\in {\mathbb{Z}}^{+}$.
14. Therefore $Q_1\ne Q_2\to x_1\ne x_2$.
15. By contrapositivity: $x_1=x_2\to Q_1=Q_2$.
16. Therefore $\forall x_1,x_2[x_1=x_2\to Q_1=Q_2]$, where $Q_1$ is created from $x_1$ and $Q_2$ is created from $x_2$
17. Therefore define $c:[0,1]\to \mathcal{Q}$ to be a mapping where on input $x$, it outputs $Q:\mathbb{I}\to \{true,false\}$ by using lines 5.1 through 5.4.
18. By lines 7, and 15, $c$ is a well-defined function since on every input, it has an output. Furthermore, on inputs $x_1=x_2$, $c(x_1)=c(x_2)$.

We’re not done! We need to argue that $c$ is injective.

Pseudo-proof:

1. Let $x_1,x_2\in [0,1]$. Assume that $c(x_1)=c(x_2)$.
2. Let $c(x_1)=Q_1$, let $c(x_2)=Q_2$.
3. Since $Q_1=Q_2$, $\forall I\in \mathbb{I}[Q_1(I)=Q_2(I)]$.
4. Now, $\forall I\in \mathbb{I}[d(b_1(f(I)))=d(b_2(f(I)))]$.
5. Since $d$ bijective, this means: $\forall I\in \mathbb{I}[b_1(f(I))=b_2(f(I))]$.
6. Assume for the sake of contradiction that $x_1\ne x_2$. Then $\exists n\in {\mathbb{Z}}^{+}$ for which $b_1(n)\ne b_2(n)$.
   1. Since $f$ is surjective, exists $I_n\in \mathbb{I}$ for which $f(I_n)=n$. Now: $b_1(f(I_n))=b_1(n)\ne b_2(n)=b_2(f(I_n))$.
   2. Contradiction, since $\forall I\in \mathbb{I}[b_1(f(I))=b_2(f(I))]$.
7. Therefore, $x_1\ne x_2$. [Negation of assumption on line 6.]

This means that $c$ is an injection from $[0,1]\to \mathcal{Q}$. So now we say “the cardinality of $[0,1]$ is less than or equals to the cardinality of $\mathcal{Q}$, the set of all computer problems”.

Ok what about the cardinality of the set of all computer problems? What is $|\mathbb{P}|$? I’m going to appeal to your intuition here. Computer programs have to be finite in length. Regardless of whether you’re writing Source, or Python, or Javascript. The program description must always be finite in length. And for the sake of simplicity, let’s say the program code can only take on 256 possible characters. ² So a code is a finite sequence of ${\mathbb{Z}}_{256}$, effectively. As a shorthand, $({\mathbb{Z}}_{256}{)}^t$ is basically a $t$ length sequence where each element in the sequence is one of $256$ possible values. Now $\mathbb{P}={\bigcup }_{t\in {\mathbb{Z}}^{+}}({\mathbb{Z}}_{256}{)}^t$. By the way, ${\bigcup }_{t\in {\mathbb{Z}}^{+}}({\mathbb{Z}}_{256}{)}^t$ is countably infinite. So, $\mathbb{P}$ is countably infinite.

So that is to say:

$$|\mathbb{P}|={\aleph }_0⪇{\aleph }_1\le |[0,1]|\le |\mathcal{Q}|$$

So what does this show? This shows there are no possible bijections between the set of computer programs $\mathbb{P}$, and the set of computer problems $\mathcal{Q}$. What does no bijection mean? We know that since $|\mathbb{P}|⪇|\mathcal{Q}|$, there is an injection from $\mathbb{P}$ to $\mathcal{Q}$ but no surjection (or else a bijection would exist). Intuitively, this means there are way more problems than there are solutions.

You might think: That’s it? We only know they exist? Can we at least solve everything that we care about? Well…

The Halting Problem

Consider the following problem:

Example

Let $P$ be a computer program, and $⟨P⟩$ denote the code of computer program $P$. For simplicity, we will think of computer programs as functions that take any string as input, and outputs $\{true,false\}$, if it terminates.

The halting problem, when set of inputs $\mathbb{I}$ is the set of all computer program code and input pairs $⟨P⟩$. I.e. $\mathbb{I}=\{(⟨P⟩,I):P\text{ is a computer program},I\text{ is input for the program}\}$. On input $(⟨P⟩,I)$, decide if $P(I)$ terminates.

Now you might think. Oh this is easy. Just take $⟨P⟩$, run the program $P(I)$, then when it outputs something, just say $true$, because it halted. But what if it doesn’t halt? How would we know?

The answer is that we actually can’t solve the halting problem in general.

Theorem

The halting problem is undecidable/uncomputable.

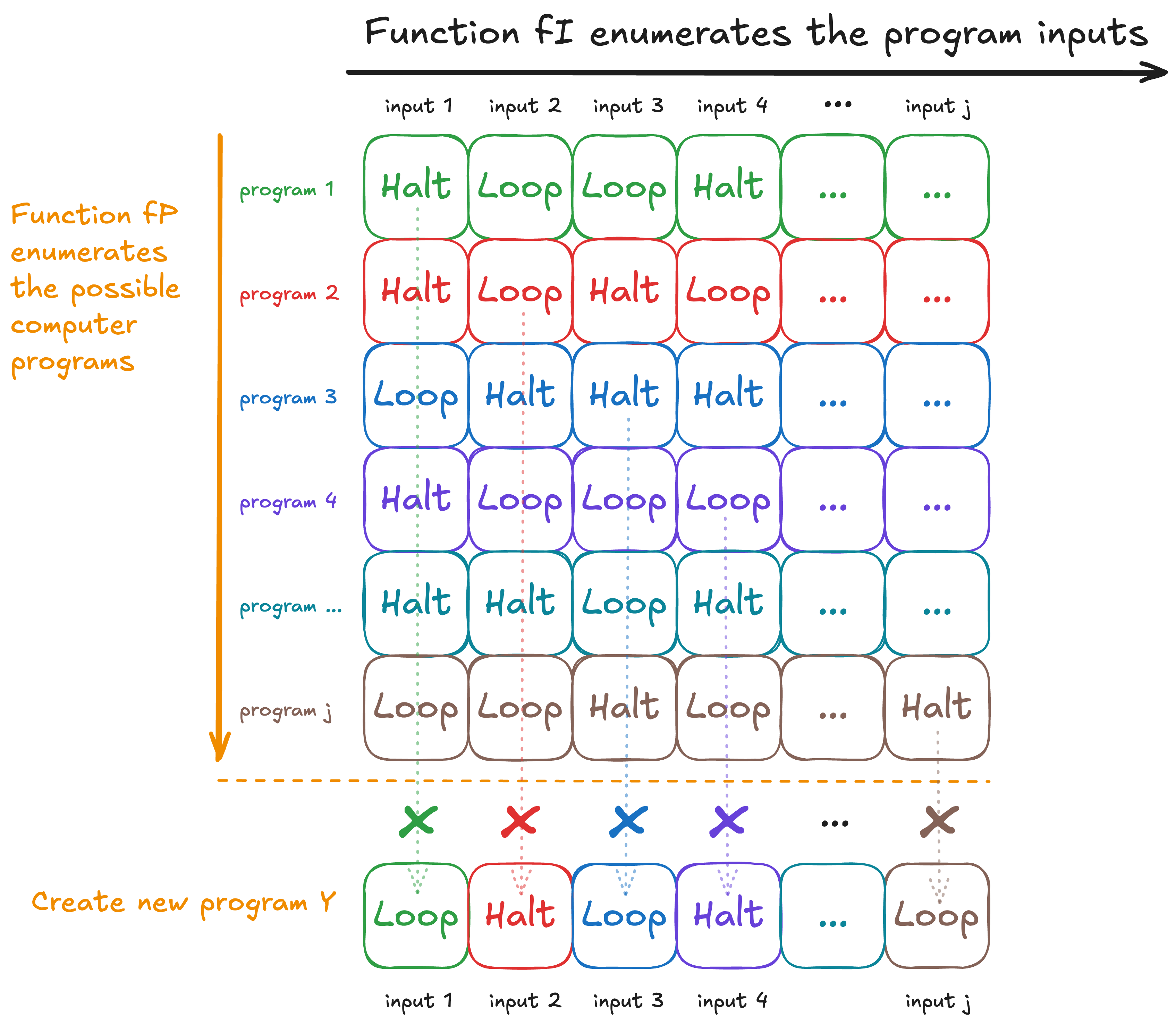
The idea is really similar to Cantor’s Diagonalisation Argument, we will assume for the sake of contradiction there is a computer program $D$ that solves this problem, we will make use of the fact that computer programs have a bijection to $\mathbb{N}$ and therefore it is a fact that every program can be enumerated in a sequence. And then assuming the existence of $D$ then we will construct a computer program $\hat{D}$ that is not enumerated in this sequence. This gives us a contraction, leading us to conclude that $D$ must not be able to exist.

Again, we will just use this very useful lemma:

Lemma

The set $\mathbb{P}$ of all computer programs $P$ has a bijection to $f_P:\mathbb{N}\to \mathbb{P}$. The set $\mathbb{I}$ of all possible computer inputs $I$ has a bijection to $f_I:\mathbb{N}\to \mathbb{I}$.

Intuitively, this is true, because every program code $⟨P⟩$ can be written as a finite sequence of characters from a finite set of characters (like ASCII). You can use the previous theorems and lemmas earlier on in the notes to basically argue that if we let ${\mathbb{P}}^i$ be the set of programs of length $P$, ${\bigcup }_{i\in {\mathbb{Z}}^{+}}{\mathbb{P}}^i$ is countably infinite, because each ${\mathbb{P}}^i$ is actually finite (It’s a finite length from finite set of characters).

Okay so again we will want to diagonalise. We want to show that if the algorithm $D$ exists, we can use it to create a new program $Y$ such that $Y$ is somehow not listed in the bijection $f_P:\mathbb{N}\to \mathbb{P}$.

Proof by contradiction

1. Assume that exists a program $D$ that solves the halting problem.
2. This means $D$ always terminates, and $D$ always outputs a correct answer when given input $⟨P⟩$ and $I$, it says $true$ if $P(I)$ terminates, and otherwise $D$ outputs $false$.
3. Create a new program $Y$ in the following way:
   1. On input $I$, since we know $f_I$ is a bijection, (handwaving a bit) we can find the number $i\in \mathbb{N}$ for which $f_I(i)=\mathbb{I}$. This step is non-trivial but it can be done.
   2. Now, $f_P(i)$ must output some program $P\in \mathbb{P}$.
   3. We will now use our assumed-to-exist halting decider $D$ to see whether $P$ halts on input $I$ or not.
   4. If $D(⟨P⟩,I)$ says $true$, then we define program $Y$ to loop forever and never terminate.
   5. Otherwise, $D(⟨P⟩,I)$ says $false$, in which case we define program $Y$ to just immediately terminate.

We now move to show that $Y$ cannot be in the output of $f_P:\mathbb{N}\to \mathbb{P}$ despite being a valid program.

4. Let’s consider the $i^{th}$ program $P=f_P(i)$ and the $i^{th}$ input $f_I(i)=I$. And we want to compare $P(I)$‘s behaviour against $Y(I)$. Notice here that if $P(I)$ were to ever terminate, then $Y(I)$ will loop forever. On the other hand, if $P(I)$ were to not terminate, $Y(I)$ would immediately terminate.
5. So $Y$ cannot be the $i^{th}$ program. But since $i$ was arbitrarily chosen, this means $Y$ cannot be the $i^{th}$ program, for all $i$. So $\forall i\in \mathbb{N}[Y\ne f_P(i)]$. But $Y$ is a valid program, we just used if-else, function-call to $D$, and looping forever can be done. And yet $f_P$ is clearly not surjective now.
6. So where’s the contradiction? We know for a fact that $f_P:\mathbb{N}\to \mathbb{P}$ must exist (it can be proven). So it was the function-call to $D$ that was problematic. i.e. Our initial assumption in this proof.

Thus, $D$ cannot exist. We cannot have a program/algorithm that looks at computer programs and see if they halt or not.

Here it is in picture form:

---

Footnotes

1. In this part we’re basically assume $\mathbb{N}$ exists already. There are axioms that we can use where $\mathbb{N}$ does not exist, and we can construct it. ↩

2. Yes I know unicode is a thing. I’m too lazy to mention how many codepoints there are etc. ↩