Unit 3: Relations

This unit introduces the notion of relations. The unit will introduce:

1. Motivation for this unit
2. Basic relations, creating relations
3. Operations on relations
4. Properties of relations

---

Part 0: Unit Introduction

In this unit, we’ll move on and extend Unit 2 on sets and talk about a special type of set, called relations.

As mentioned, one of the biggest reasons for knowing set operations and relations has to do with databases. It is not the only motivation, but in my opinion it is one of the the most immediately motivating topics for why students of computer science should study set theory and relations. Another deeper reason presents itself in distributed systems, and a lot of the language of relations is very useful there as well.

That being said, relations are interesting for other reasons in their own right for discrete mathematics as well. This unit will talk about relations, cover basic terminology and concepts, and show you how they are useful for databases and distributed systems. Again, the unit will start with terminology, and basic concepts, and end on proofs about such concepts.

Motivating Relations

Our starting point is to talk about what a relation is. And there are two separate ways to motivate this. Let’s talk about both ways:

Application 1: Databases

Let’s say that you had to represent some data. We’ve already seen some examples of this at the start and end of Unit 2 on sets, but let’s try to motivate why data is organised that way. (While TCX1004 is not a course on databases, I think all the same it is great to talk about the relational data model here. You won’t learn about databases until TCX2003, but seeing this in advance won’t hurt.)

Let’s say we collected some data about people and their email addresses, perhaps via survey or something. So here’s the example table we had again:

Name	Email
Jon Snow	jsnow@gmail.com
Barry Allen	the_flash@hotmail.com
Pikachu	pika@pokemail.com

One way to see this is that we actually have 3 pairs from a set that looks something like this:

$$Data=Names\times Emails$$

where $Data$ is a set that is the Cartesian product of two sets, $Names$ and $Email$. Here, let’s pretend that $Names$ contains all the possible names in the world, and $Emails$ also contains all the possible email addresses we have in the world.

Based on this terminology, we can say something like $(JonSnow,jsnow@gmail.com)\in Data$. Similarly, we can say $(BarryAllen,the\_flash@hotmail.com)\in Data$.

Here in set theory terminology, something like $(JonSnow,jsnow@gmail.com)$ is called a pair. It is also called a 2-tuple.

Importantly, we can call this a relation. Why? We are relating the names to emails—we are establishing an association, or a relationship between someone’s name and their email.

This way of representing data is called the relational model by people who study and use databases. The concept was coined by Dr. Edgar F. Codd. In some sense, he took the concept of relations in mathematics and decided to use it to represent data. You will see why the model is useful in a class on databases. We are just using this real-life example as a motivation on why understand relations. In the previous unit, we talked about set operations, and those are very much applicable in a database setting. Since to (union / intersect / set minus) your data is a very common form of data manipulation. (See the bonus section at the end of Unit 2.)

Application 2: How to represent orderings

Putting the cart before the horse for a little bit (showing you how and why it’s used before showing you the concept), one big application from a mathematical perspective is the ability to talk about orderings among objects. There is probably one you’re quite familiar with: ordering numbers from sets like $\mathbb{N},\mathbb{Z},$ or $\mathbb{R}$ using $\le$. Perhaps that seems quite uninteresting, but understanding how to “order” or how to “sort” objects is actually quite a huge area of study, and has found its way into computer science as well in the last one or two decades.

If you ever find yourself studying memory models for concurrency-based applications, or designing a distributed systems algorithm, chances are you will have to know a little bit about partial orders (as special type of relation). The vague idea is that when you need to start saying things like “this memory event happened before the other memory event”, that is also a kind of ordering.

---

Part 1: Basic Relations, Creating Relations

Definition of a Relation

Let’s think a little bit about how to “relate” two objects (again, using the example from earlier and from the previous unit). If we want to relate people to their emails, then we can think of creating pairs to do this. For example, we might represent our data like this:

Name	Email
Jon Snow	jsnow@gmail.com
Barry Allen	the_flash@hotmail.com
Pikachu	pika@pokemail.com

Mathematically, we will see this our table (let’s call it $T$) as a set of three pairs:

$$\begin{array}{rl}T=\{& \\ & (JonSnow,jsnow@gmail.com),\\ & (BarryAllen,the\_flash@hotmail.com),\\ & (Pikachu,pika@pokemail.com)\\ \}& \end{array}$$

Notice here that if we let $N$ be the set of all possible names and let $E$ be the set of all possible emails, then $T\subseteq N\times E$. Note that it is not necessarily the case that $T=N\times E$. $T$ here only contains certain pairs from $N\times E$, not all of them!

$T$ here is a relation that relates elements from $N$ to elements in $E$. A relation is really just a set that tells us how objects and $N$ and $E$ are associated.

Here’s another example—we could have had a table of student data that includes:

1. Their name
2. Their year of enrolment
3. Their degree

Perhaps something like this:

Name	Year of Enrolment	Degree
Simon	2023	CS
Janice	2020	Philo
Meg	2015	CS
Sam	2016	Science

Then we could have represented this using a set $S$ like so:

$$\begin{array}{rl}S=\{& \\ & (Simon,2023,CS),\\ & (Janice,2020,Philo),\\ & (Meg,2015,CS)\\ & (Sam,2016,Science)\\ \}& \end{array}$$

like a set of triples. But what if we wanted two sets $A$ and $B$ that represented the following relations?

1. Set $A$ relates the student names to the year of enrolments.
2. Set $B$ relates the student names to the degree programmes.

Try for yourself to write down what those sets look like, and what they are subsets of. Check it with yourself in the hidden-away spoiler tag. We can let $M$ be the set of all possible names, and we can let $P=\{CS,Philo,CS,Science,Eng,Biz\}$.

Answer

$A$ can be a subset of something like $M\times \mathbb{N}$. Based on our data, it can also be a subset of something like $M\times \{2015,2016,2020,2023\}$. Both answers are viable.

$$A=\{(Simon,2023),(Janice,2020),(Meg,2015),(Sam,2016)\}$$

Answer

$B$ can be a subset of something like $M\times P$.

$$B=\{(Simon,CS),(Janice,Philo),(Meg,CS),(Sam,Science)\}$$

Definition: Relations

Let $A$ and $B$ be two sets.

A set of pairs $R$ is called a relation (on sets $A$ and $B$) if it is a subset of the Cartesian product of the sets, i.e., $R\subseteq A\times B$.

Alternatively, any set of pairs is a relation.

Formally, we will consider any set that is a subset of some Cartesian product of sets to be a relation on those two sets. Alternatively, any set of pairs is a relation.

Here are a few more examples:

Example

Let’s say $F$ is the set of all possible foods, and $P$ is the set of all possible people. Then we can have a set $S$ that is a relation between people and the food they enjoy eating.

$$S=\{(Jane,Laksa),(Marco,Toast),(Jane,Pasta),(Sam,Toast)\}$$

Notice here that we can relate one person to more than one food. We can also relate more than one person to one food. In general, since $S$ is a subset of $P\times F$, it is considered a relation.

Example

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[x\cdot k=y]\}$.

Then $D$ relates integers $y$ to other integers that divide it. For example $(2,10)\in D$, because $2$ divides $10$. Also $(3,10)\notin D$, because $3$ does not divide $10$.

Example

Let $M=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=3t]\}$.

Then $M$ relates integers $a$ to integers $b$ if they have the same divisor when divided by $3$. For example, $(7,16)\in M$ because both have the remainder $1$ when divided by $3$. Similarly, $(27,6)\in M$ because both have the remainder $0$. Meanwhile, $(3,11)\notin M$ because $3$ has remainder $0$, but $11$ has remainder $2$.

Question

What about if we wanted to relate three things together? You will see this very commonly in databases. It is called a ternary relation. In general, a relation that relates $n$ things is called an $n$-ary relation.

For the purposes of our course, we will focus only on binary relations, i.e., sets of pairs only.

---

Part 2: Operations on Relations

Just like sets, there are a few common operations that we need to learn for relations. We will cover the two most common ones:

1. Relation inversion
2. Relation composition

Relation Inversion

Definition: Relation inversion

Given a relation $R\subseteq A\times B$, the inversion of a relation, denoted $R^{-1}$, is defined by

$$R^{-1}=\{(b,a)\in B\times A:(a,b)\in R\}$$

Basically, it is just saying that a pair $(b,a)$ is in $R^{-1}$ if and only if $(a,b)$ is in $R$. Think of $R^{-1}$ as just “reversing” the pairs in $R$.

Let’s see what this means for our previous three examples.

Example

Let’s say $F$ is the set of all possible foods, and $P$ is the set of all possible people, then we can have a set $S$ that is a relation between people and the food they enjoy eating. Previously, we gave an example of such a set.

$$S=\{(Jane,Laksa),(Marco,Toast),(Jane,Pasta),(Sam,Toast)\}$$

Then:

$$S^{-1}=\{(Laksa,Jane),(Toast,Marco),(Pasta,Jane),(Toast,Sam)\}$$

Example

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[x\cdot k=y]\}$.

Recall that $(2,10)\in D$, because $2$ divides $10$. Also $(3,10)\notin D$, because $3$ does not divide $10$.

For example, $(10,2)\in D^{-1}$ and $(10,3)\notin D^{-1}$.

Example

Let $M=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=3k]\}$.

Since $(7,16)\in M$, this means that $(16,7)\in M^{-1}$. For the same reason, $(6,27)\in M^{-1}$. Also, since $(3,11)\notin M$, we have that $(11,3)\notin M$.

Relation Composition

Next is the relation composition operation. This one is slightly involved, so let me start with a few examples.

Example 1

Let’s say we had a set that relates locations via bus routes. Set $A$ might relate the stops of the 284 bus service. We will say $(a,b)\in A$ if bus stop $a$ is directly before stop $b$.

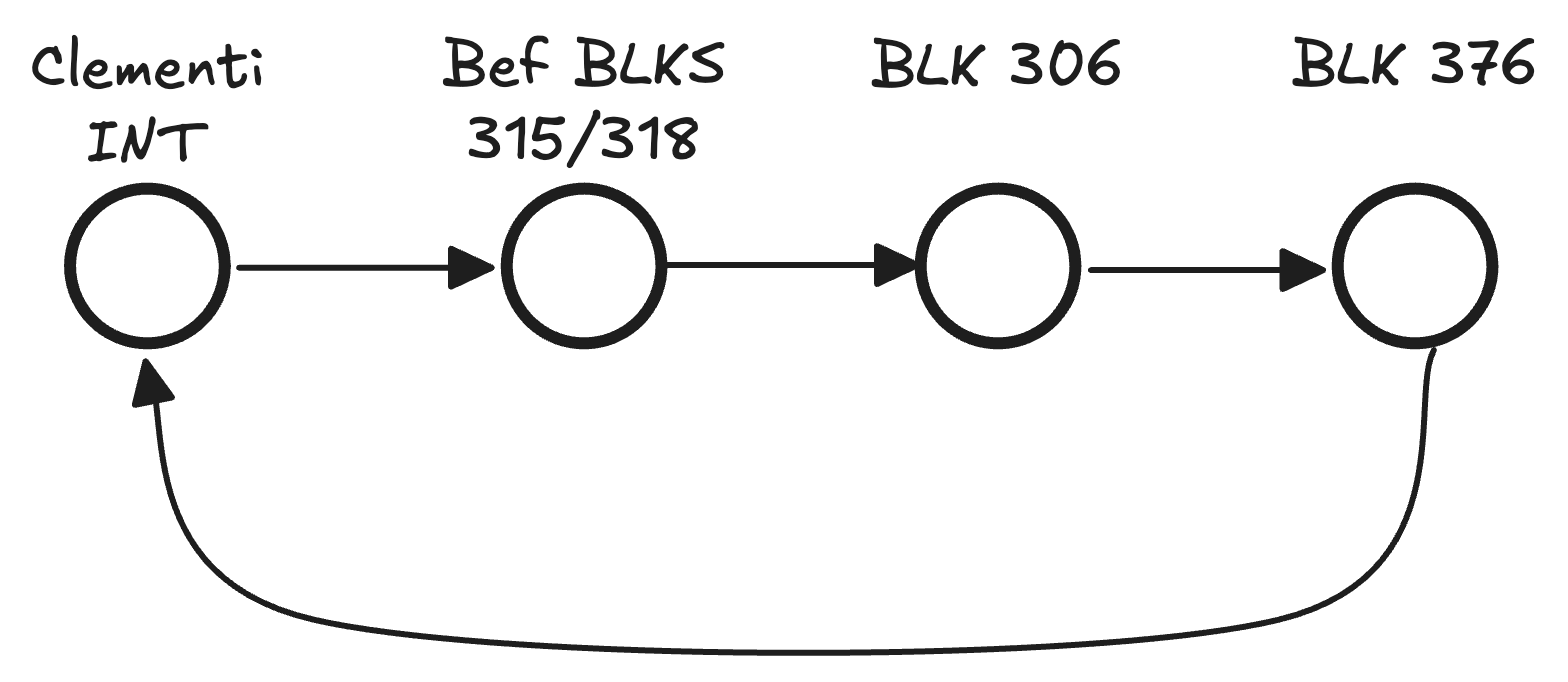
For example, $A$ looks something like this:

$$\begin{array}{rl}A=\{& \\ & (ClementiINT,BefBlks315/318),\\ & (BefBlks315/318,BLK306),\\ & (BLK306,BLK376),\\ & (BLK376,ClementiINT)\\ \}& \end{array}$$

What if we wanted to say that we wanted to take the 284 bus for exactly two stops? We could write this as the composition of $A$ with $A$, denoted by $A;A$. And it is such that:

$$\begin{array}{rl}A;A=\{& \\ & (ClementiINT,BLK306),\\ & (BefBlks315/318,BLK376),\\ & (BLK306,ClementiINT)\\ & (Blk376,BefBlks315/318)\\ \}& \end{array}$$

Notice how the reason $(ClementiINT,BLK306)\in A;A$ was because there was some value $x$, such that $(ClementiINT,x)\in A$ and also $(x,BLK308)\in A$. (Namely, $x=BefBlks315/318$.)

Example 2

Let’s try another example, this time around let’s make a set $E$ that relates any two MRT stations that are connected via the East-West line. This is different from the previous example, but an equally valid way to make a relation. For example, $(CityHall,Clementi)\in E$ (even if they are not directly next to each other).

Let’s also make another set $N$ that relates any two MRT stations that are connected via the North-South line. For example, $(ToaPayoh,CityHall)\in N$.

Okay, so this time around, we have two different relations. Think a little bit about what the relation $N;E$ represents.

$N;E$ relates two MRT stations $(s_1,s_2)$ if we can start from a station $s_1$ that is on the North-South line, and $s_2$ is a station that is on the East-West line.

So for example, $(Yishun,Bedok)\in N;E$. But something like $(Redhill,YewTee)\notin N;E$. Also, something like $(CityHall,RafflesPlace)\in N;E$. Can you see why?

Pictorially, here’s what’s going on:

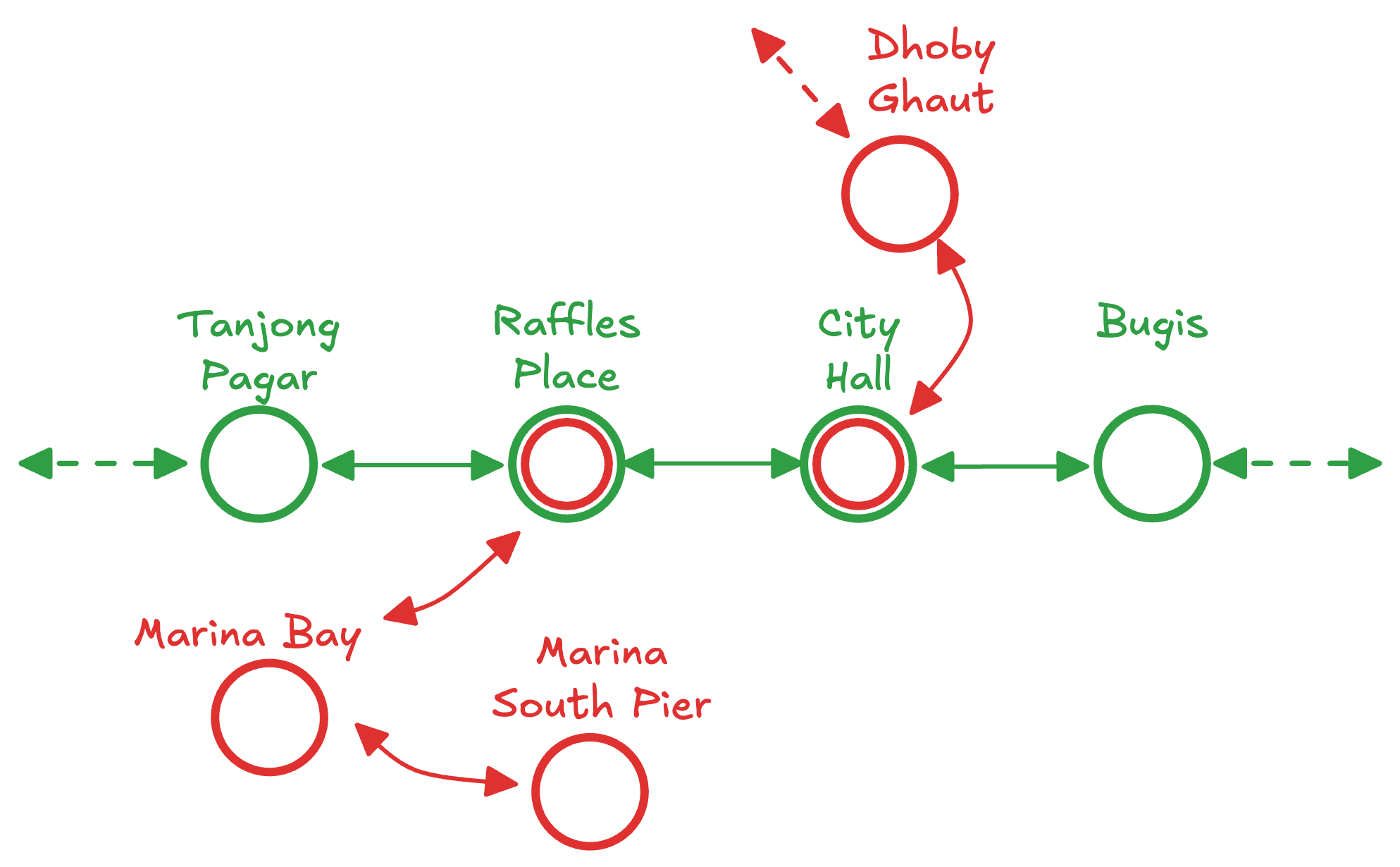
We can say something like $(DhobyGhaut,TanjongPagar)\in N;E$, because we know $(DhobyGhaut,CityHall)$ is in $N$ and $(CityHall,TanjongPagar)$ is in $E$.

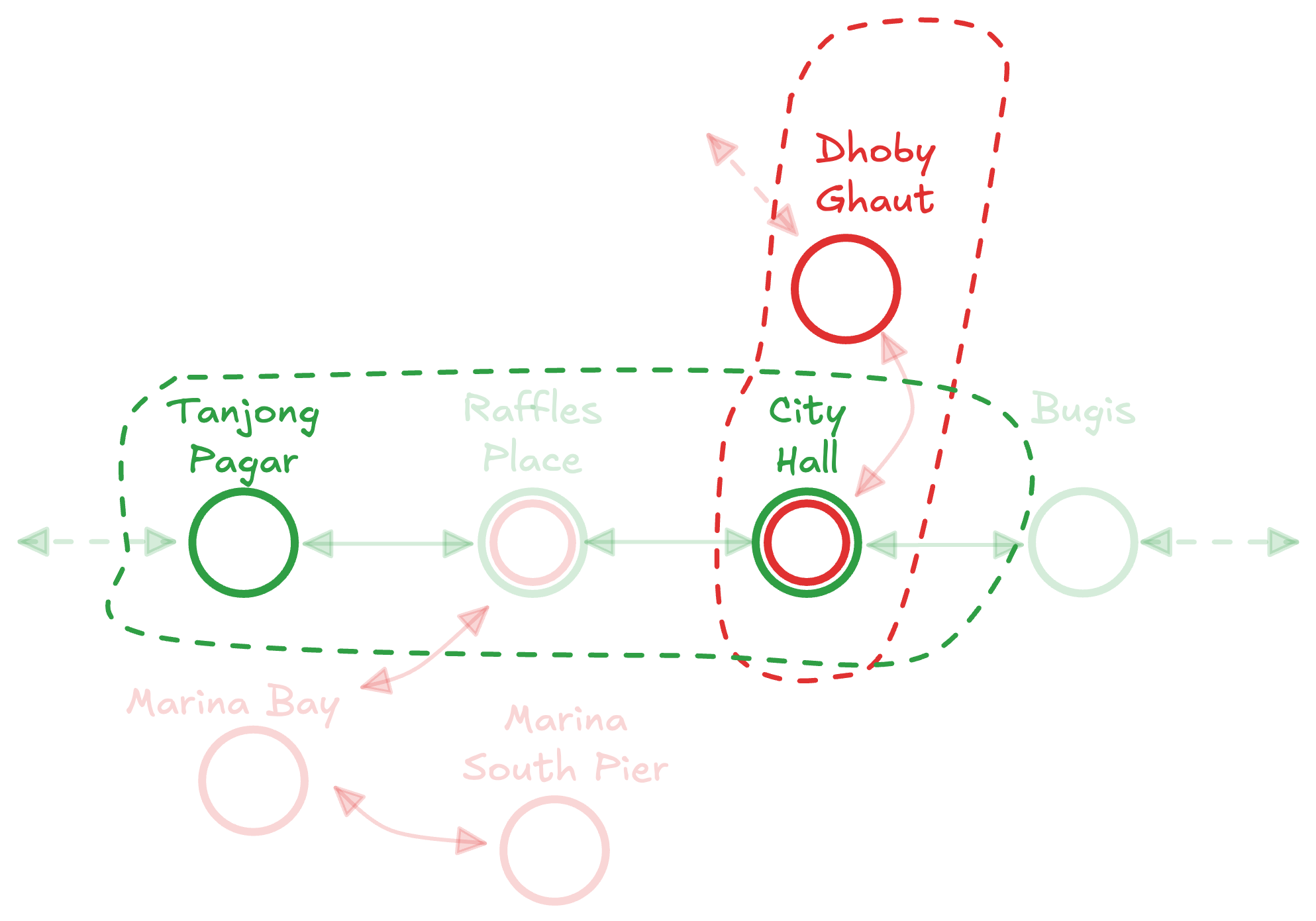
Definition: Relation composition

Let $R\subseteq A\times B$ and $S\subseteq B\times C$ be two relations. The composition of $R$ and $S$, denoted $R;S$, is defined by:

$$R;S=\{(a,c)\in A\times C:\exists b\in B[(a,b)\in R\wedge (b,c)\in S\left]\right\}$$

In English, this is basically just saying:

$a$ and $c$ are related by $R;S$ if we can find a $b\in B$ such that $a$ is related to this $b$ by relation $R$, and the same $b$ is related to $c$ by relation $S$.

If no such $b$ exists, then $a$ and $c$ are not related by $R;S$.

You can mentally picture this as “Taking one step using $R$, and then taking one step using $S$.”

So let’s go back through the examples we had, and see what happens.

Example

Let’s say $F$ is the set of all possible foods, and $P$ is the set of all possible people, then we can have a set $S$ that is a relation between people and the food they enjoy eating. Previously, we gave an example of such a set.

$$S=\{(Jane,Laksa),(Marco,Toast),(Jane,Pasta),(Sam,Toast)\}$$

Then,

$$S;S=\varnothing$$

Example

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[x\cdot k=y]\}$.

For example, since $(5,10)\in D$, and $(10,200)\in D$, then $(5,200)\in D;D$.

Do you notice something interesting? In general, we can actually notice that if $x$ divides $y$, and $y$ divides $z$, then $x$ divides $z$ (this can be proven). So we can actually argue that if $(a,b)\in D$ then $(a,b)\in D;D$. In other words, $D\subseteq D;D$.

Example

Let $M=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=3k]\}$.

Since $(3,27)\in M$ and $(27,51)\in M$, we can say $(3,51)\in M;M$.

Example

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[x\cdot k=y]\}$, and $M=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=3k]\}$.

Then $(2,8)\in D$ and $(8,14)\in M$, so $(2,14)\in D;M$.

Classic Examples of Relations

Before moving on, we’ve been commonly using some relations that are good examples for the remaining concepts that we want to talk about, so let’s explicitly give them names here first.

Example 1: Divisibility

Let the set $D$ be such that:

$$D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=y)]\}$$

Then we will call $D$ the divisibility relation. Here we will only consider natural numbers. For instance, $(2,10)\in D$ and $(3,60)\in D$, but $(60,3)\notin D$ and $(2,3)\notin D$.

Example 2: Congruence modulo $n$

Let us fix $n\in \mathbb{N}$, and let the set $C_n$ be a relation be such that:

$$C_n=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=n\cdot k]\}$$

We call $C_n$ the congruence modulo $n$ relation. Intuitively, two integers $(x,y)$ are related by $C_n$ if they share the same remainder when divided by $n$.

Again, $(5,14)$ are related via relation $C_3$, but not via relation $C_5$. On the other hand, $(6,11)$ is not related via relation $C_3$, but are related via relation $C_5$.

---

Part 3: Properties of Relations

As you might have noticed, relations by themselves as just sets of pairs are nothing special. However, there are certain properties that certain relations might have. In this section, we will go through them. For this section, we shall restrict our attention to relations $R$ of the form $R\subseteq A\times A$. In other words, they relate items in the same set $A$. (We will not be considering relations $R\subseteq A\times B$, where $A\ne B$.)

Property 1: Reflexivity

Definition: Reflexivity

A relation $R\subseteq A\times A$ is reflexive if and only if

$$\forall a\in A[(a,a)\in R]$$

Here’s a pictorial example:

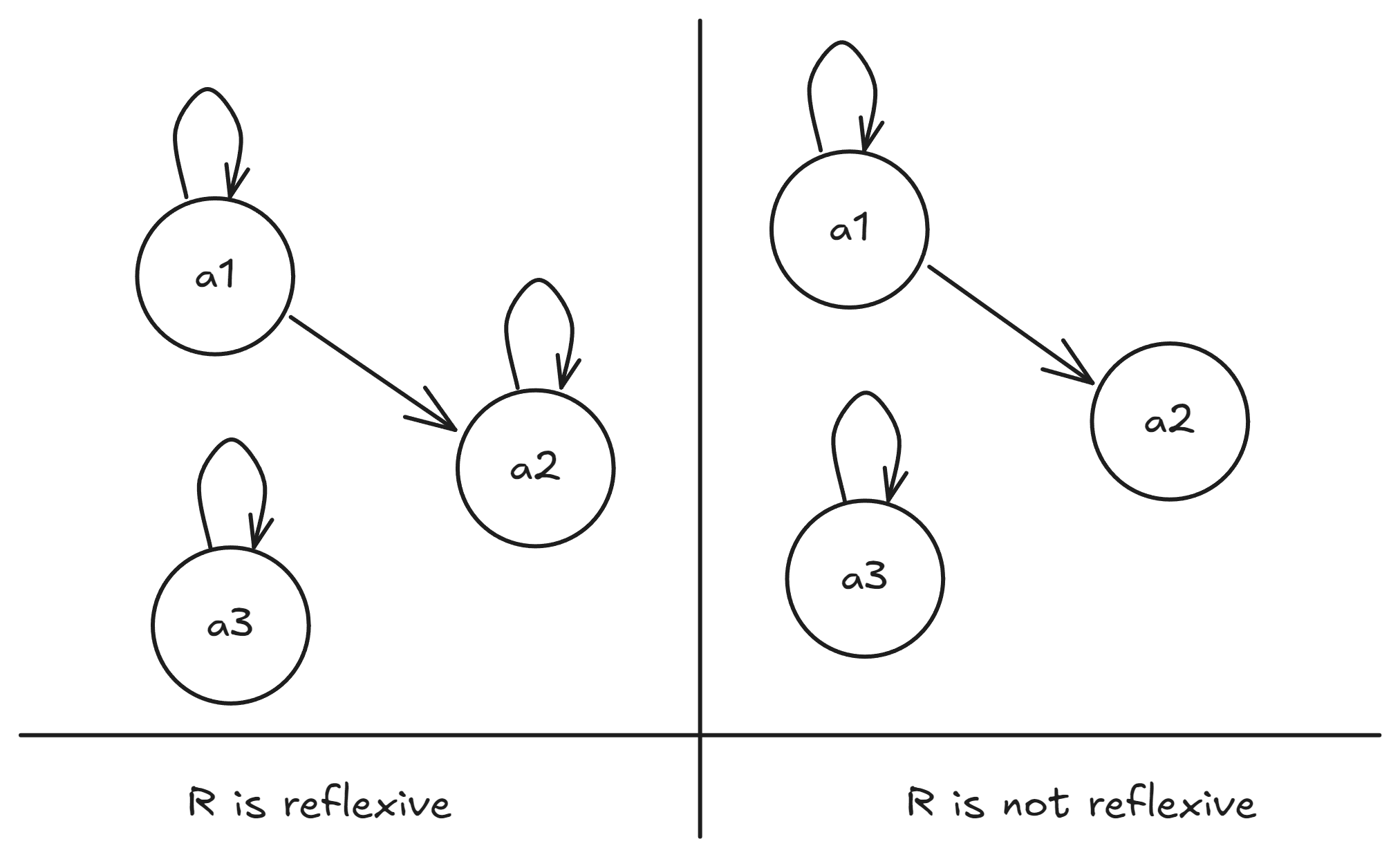
Let $A=\{a_1,a_2,a_3\}$. Then the relation on the left is $\{(a_1,a_1),(a_2,a_2),(a_3,a_3),(a_1,a_2)\}$. Since every element of $A$ is related to itself, i.e., $\forall a\in A[(a,a)\in R]$ (notice that in the picture there are self-loops from each element of $A$), the relation on the left is reflexive. Also notice that $(a_1,a_2)$, but that is irrelevant. We are only concerned with whether every element is related to itself.

On the other hand, the relation on the right is not reflexive. Why? The relation on the right can be written as $\{(a_1,a_1),(a_3,a_3),(a_1,a_2)\}$. Notice that $a_2\in A$ and yet $(a_2,a_2)\notin R$, so we can say that $\exists a\in A[(a,a)\notin R]$, which as we know, is equivalent to $\neg (\forall a\in A[(a,a)\in R\left]\right)$. This again confirms that the relation on the right is not reflexive. The pictorial intuition is that some element is missing a self-loop.

So let’s examine the two special relations from before and see if they are reflexive.

Divisibility is reflexive

Is the divisibility relation reflexive? Yes. After all, every number divides itself. Let’s see a proof of this.

Theorem

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=y)]\}$.

Then $D$ is reflexive.

Proof

1. Let $x\in \mathbb{N}$ be arbitrarily chosen.
2. $x\cdot 1=x$ [Basic algebra]
3. $1\in \mathbb{Z}$ [Basic algebra]
4. $1\ne 0$ [Basic algebra]
5. $(1\ne 0)\wedge (x\cdot 1=x)$ [Conjunction of lines 2 and 4]
6. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=x)]$ [Existential generalisation on lines 2, 3]
7. $x\in \mathbb{N}\wedge (\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=x)\left]\right)$ [Conjunction on lines 1 and 6]
8. $(x,x)\in D$ [Definition of $D$]
9. $\forall x\in \mathbb{N}[(x,x)\in D]$ [Universal generalisation on lines 1 and 8]

So the divisibility relation $D$ is reflexive!

Congruence is reflexive

What about congruence modulo $n$ relation? Fix $n\in \mathbb{N}$—our goal statement is to show that $\forall x\in \mathbb{Z}[(x,x)\in C_n]$.

Theorem

Let $C_n=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=n\cdot k]\}$.

Then $C_n$ is reflexive.

Proof

1. Let $x\in \mathbb{Z}$ be arbitrarily chosen.
2. $x-x=0=n\cdot 0$ [Basic algebra]
3. $0\in \mathbb{Z}$ [Basic algebra]
4. $\exists k\in \mathbb{Z}[(x-x)=n\cdot k]$ [Existential generalisation on lines 3 and 4]
5. $x\in \mathbb{Z}\wedge (\exists k\in \mathbb{Z}[(x-x)=n\cdot k\left]\right)$ [Conjunction on lines 1 and 4]
6. $(x,x)\in C_n$ [Definition of $C_n$]
7. $\forall x\in \mathbb{Z}[(x,x)\in C_n]$ [Universal generalisation on lines 1 and 6]

So the divisibility relation $C_n$ is also reflexive!

Here’s an example of a relation that is not reflexive. Let $A=\{(x,y)\in \mathbb{Z}\times \mathbb{Z}:x+1=y\}$. So for example, $(5,6)$ are related by $A$, but $(6,6)$ and $(5,5)$ are not related by $A$. How do we prove this? Our goal statement is to show that $\neg (\forall x\in \mathbb{Z}[(x,x)\in A\left]\right)$.

Proof

1. $5+1\ne 5$ [Basic algebra]
2. $5\in \mathbb{Z}$ [Basic algebra]
3. $\neg (5+1=5)$ [Logically equivalent to line 1]
4. $(5,5)\notin A$ [Definition of $A$]
5. $\exists x\in \mathbb{Z}[(x,x)\notin A]$ [Existential generalisation on lines 2 and 4]
6. $\neg (\forall x\in \mathbb{Z}[(x,x)\in A\left]\right)$ [Logically equivalent to line 5]

Property 2: Symmetry

Definition: Symmetry

A relation $R\subseteq A\times A$ is symmetric if and only if

$$\forall a\in A,\forall b\in A[(a,b)\in R\to (b,a)\in R]$$

In English:

For all possible $a\in A$ and $b\in B$, if $a$ is related to $b$ via relation $R$, then $b$ must be related to $a$ via relation $R$ too.

Notice here this means that if we chose some values $a$ and $b$ such that $a$ is not related to $b$, we don’t care whether $b$ is related to $a$ or not.

Here’s a pictorial example:

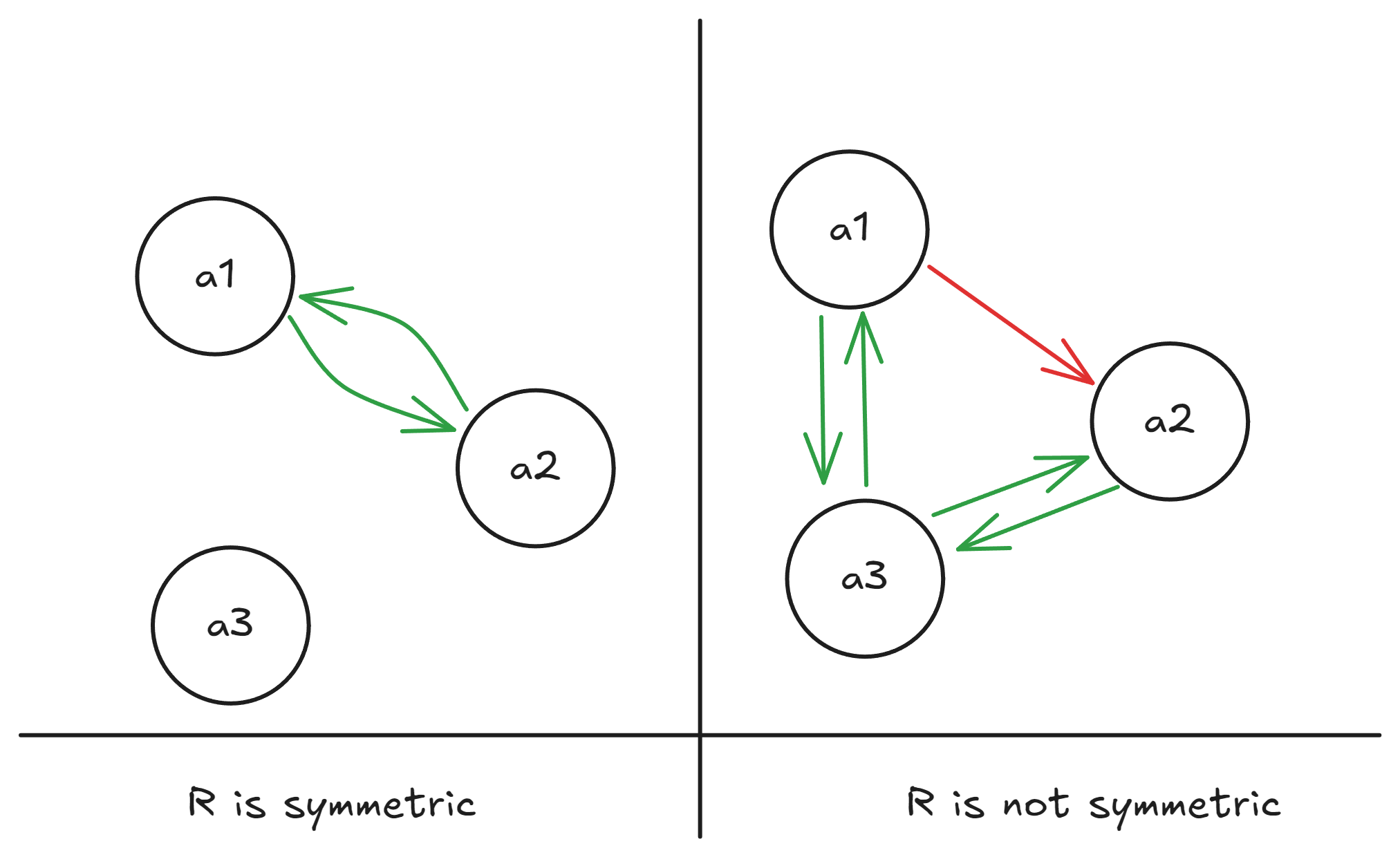
Let $A=\{a_1,a_2,a_3\}$. Then the relation on the left is $\{(a_1,a_2),(a_2,a_1)\}$. Notice that since $a_1$ is related to $a_2$, then we must have that $a_2$ is related to $a_1$ in order for this relation to be symmetric. Similarly, since $a_2$ is related to $a_1$, we must have $a_2$ is related to $a_1$ for this relation to be symmetric. Since both of these are true, we conclude that the relation on the left is indeed symmetric.

On the other hand, the relation on the right is $\{(a_1,a_3),(a_3,a_1),(a_3,a_2),(a_2,a_3),(a_1,a_2)\}$. Notice there that $a_1$ is related to $a_2$, but $a_2$ is not related to $a_1$. So now we can say:

$$\exists a\in A,\exists b\in A[(a,b)\in R\wedge (b,a)\notin R]$$

which is logically equivalent to:

$$\exists a\in A,\exists b\in A[\neg ((a,b)\in R\to (b,a)\in R\left)\right]$$

which is also logically equivalent to:

$$\neg (\forall a\in A,\forall b\in A[(a,b)\in R\to (b,a)\in R\left]\right)$$

which means that the relation on the right is not symmetric.

Divisibility is not symmetric

So is the divisibility relation symmetric? Well, we can think about this intuitively first. If we know that some integer $a$ divides some integer $b$, does this mean that $b$ divides $a$? Let’s think about what happens when $a=5$ and $b=10$. Indeed $a$ does divide $b$, but $b$ does not divide $a$.

Using the similar reasoning as before, this means that the divisibility relation is not symmetric.

Congruence is symmetric

What about the congruence modulo $n$ relation $C_n$? Intuitively, $a$ and $b$ are related because they have the same remainder modulo $n$, so of course it doesn’t matter if we said $a$ or $b$ first.

Let’s look at the formal proof now.

Theorem

Let $C_n=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=n\cdot k]\}$.

Then $C_n$ is symmetric.

Proof

1. Let $a\in \mathbb{Z}$ be arbitrarily chosen.
2. Let $b\in \mathbb{Z}$ be arbitrarily chosen.
3. Assume $(a,b)\in C_n$.
   1. $\exists k\in \mathbb{Z}[a-b=n\cdot k]$ [Definition of $C_n$]
   2. Let $t\in \mathbb{Z}$ be such that $[a-b=n\cdot t]$. [Existential instantiation on line 3.1]
   3. $(b-a)=-(a-b)=(-t)\cdot n$ [Basic algebra]
   4. $-t\in \mathbb{Z}$ [Basic algebra]
   5. $\exists k\in \mathbb{Z}[b-a=n\cdot k]$ [Existential instantiation on line 3.5]
   6. $(b,a)\in C_n$ [Definition of $C_n$]
4. $(a,b)\in C_n\to (b,a)\in C_n$ [Implication introduction on lines 3 and 3.6]
5. $\forall b\in \mathbb{Z}[(a,b)\in C_n\to (b,a)\in C_n]$ [Universal generalisation on lines 2 and 4]
6. $\forall a\in \mathbb{Z},\forall b\in \mathbb{Z}[(a,b)\in C_n\to (b,a)\in C_n]$ [Universal generalisation on lines 1 and 5]

Property 3: Anti-Symmetry

Definition: Anti-symmetry

A relation $R\subseteq A\times A$ is anti-symmetric if and only if

$$\forall a\in A,\forall b\in A\left[\right((a,b)\in R\wedge (b,a)\in R)\to a=b]$$

In English:

For all possible $a\in A$ and $b\in B$, if ($a$ is related to $b$ via relation $R$, and also $b$ is related to $a$ via relation $R$) then $a=b$.

That’s the standard way that is it written, but I find that confusing for newcomers. We can instead write it as the following (since it is logically equivalent):

$$\forall a\in A,\forall b\in A[a\ne b\to ((a,b)\notin R\vee (b,a)\notin R\left)\right]$$

which in English:

For all possible $a\in A$ and $b\in B$, if $a\ne b$, then either $a$ is not related to $b$, or $b$ is not related to $a$.

This pretty much tells you that for an anti-symmetric relation, the only time that $a$ and $b$ can be related to each other is when $a=b$.

Here’s a pictorial example:

A relation on the left is anti-symmetric because the only time $a$ and $b$ are related are either: when $a=b$, or when the relation is “one-sided”. For instance, $a_1$ is related to $a_2$ but not the other way around.

On the other hand, for the relation on the right, $a_2$ is related to $a_3$ and $a_3$ is related to $a_2$, but $a_2$ is not the same as $a_3$. Hence, the relation on the right is not anti-symmetric.

Divisibility is anti-symmetric

Is the divisibility relation anti-symmetric? Here’s the intuition: If we know that $a$ divides $b$, and we also know that $b$ divides $a$, then the only possible case is that $a=b$. Here’s the proof that confirms this:

Theorem

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=y)\left]\right\}$.

Then $D$ is anti-symmetric.

Proof

1. Let $a\in \mathbb{N}$ be arbitrarily chosen.
2. Let $b\in \mathbb{N}$ be arbitrarily chosen.
3. Assume that $(a,b)\in D\wedge (b,a)\in D$.
   1. $(a,b)\in D$ [Specialisation on line 3]
   2. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (a\cdot k=b)]$ [Definition of $D$]
   3. Let $t_1\in \mathbb{Z}$ such that $(t_1\ne 0)\wedge (a\cdot t_1=b)$. [Existential instantiation on line 3.2]
   4. $a\cdot t_1=b$ [Specialisation on line 3.3]
   5. $(b,a)\in D$ [Specialisation on line 3]
   6. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (b\cdot k=a)]$ [Definition of $D$]
   7. Let $t_2\in \mathbb{Z}$ such that $(t_2\ne 0)\wedge (b\cdot t_2=a)$. [Existential instantiation on line 3.6]
   8. $b\cdot t_2=a$ [Specialisation on line 3.7]
   9. $b=a\cdot t_1=(b\cdot t_2)\cdot t_1$ [Basic algebra]
   10. $t_1\cdot t_2=1$ [Basic algebra]
   11. $t_1=1$ [Basic algebra, because $t_1,t_2$ are natural numbers]
   12. $a=a\cdot 1=a\cdot t_1=b$ [Basic algebra]
4. $((a,b)\in D\wedge (b,a)\in D)\to a=b$ [Implication introduction on lines 3, 3.12]
5. $\forall b\in \mathbb{Z}\left[\right((a,b)\in D\wedge (b,a)\in D)\to a=b]$ [Universal generalisation on lines 2 and 4]
6. $\forall a\in \mathbb{Z},\forall b\in \mathbb{Z}\left[\right((a,b)\in D\wedge (b,a)\in D)\to a=b]$ [Universal generalisation on lines 1 and 5]

Congruence is not anti-symmetric

What about the congruence modulo $n$ relation $C_n$? This one is probably quite straightforward. Let’s give an example: consider $3$ and $0$. They are related via $C_3$ (both $3$ is related to $0$, and $0$ is related to $3$), but $3\ne 0$. So $C_3$ is not anti-symmetric. The same idea works for any $C_n$.

Property 4: Transitivity

Definition: Transitivity

A relation $R\subseteq A\times A$ is transitive if and only if

$$\forall a\in A,\forall b\in A,\forall c\in A\left[\right((a,b)\in R\wedge (b,c)\in R)\to (a,c)\in R]$$

In English:

If $a$ is related to $b$, and $b$ is related to $c$, then $a$ is related to $c$.

The quickest example that demonstrates this idea is the concept of $\le$. If we know that $a\le b$, and we know that $b\le c$, then we know that $a\le c$. So $\le$ is actually a transitive relation.

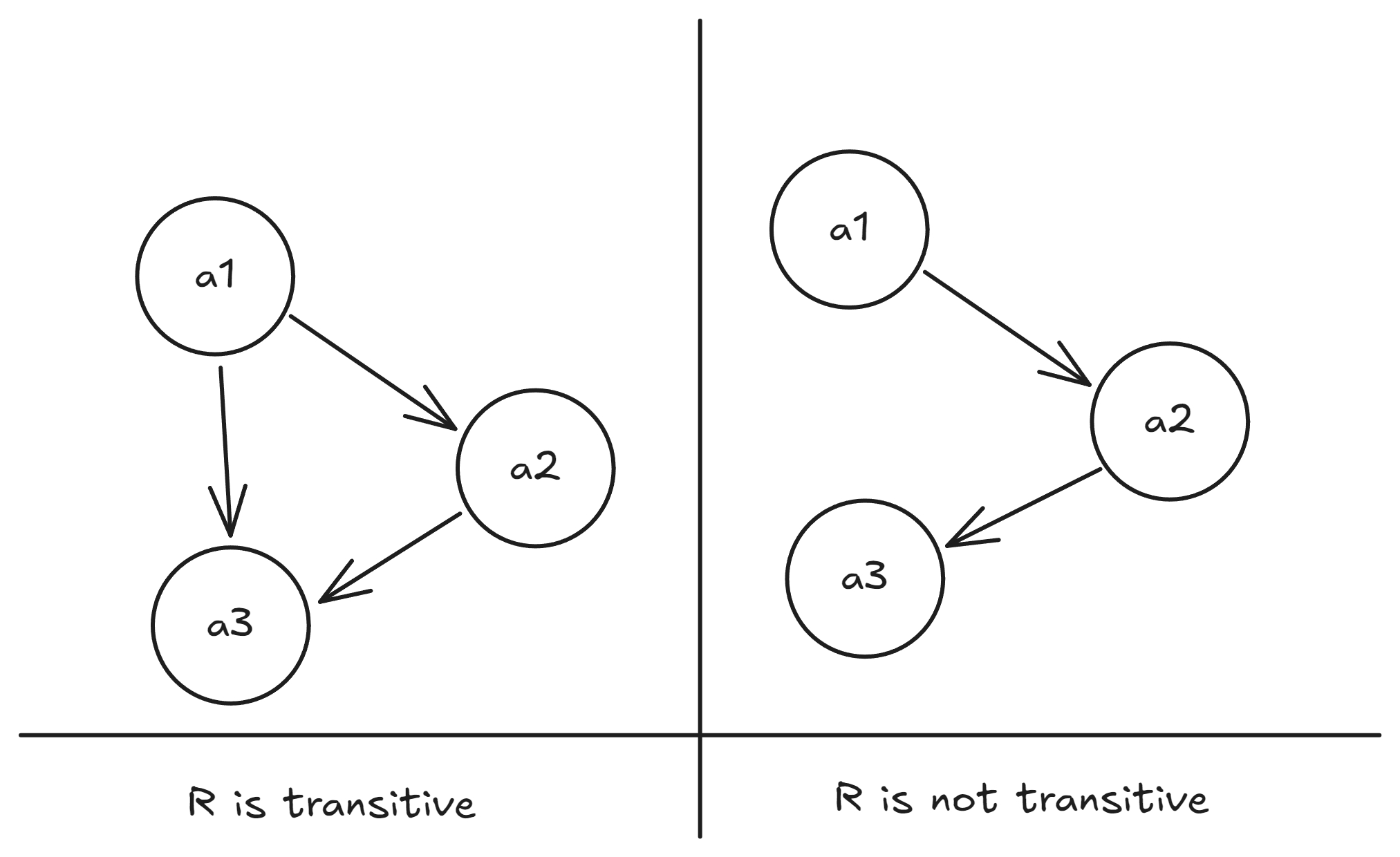
Pictorially, because both $(a_1,a_2)$ and $(a_2,a_3)$ are related, we must have that $(a_1,a_3)$ are related too, in order for the relation to be transitive. Hence, the relation on the left is transitive. However, on the right side, both $(a_1,a_2)$ and $(a_2,a_3)$ are related, but $(a_1,a_3)$ are not related, so the relation is not transitive.

To be clear, something like the following relations are also transitive:

Let’s end the chapter by proving our two usual examples of relations are both transitive.

Divisibility is transitive

Theorem

Let $D=\{(x,y)\in \mathbb{N}\times \mathbb{N}:\exists k\in \mathbb{Z}[(k\ne 0)\wedge (x\cdot k=y)]\}$.

Then $D$ is transitive.

Proof

1. Let $a\in \mathbb{N}$ be arbitrarily chosen.
2. Let $b\in \mathbb{N}$ be arbitrarily chosen.
3. Let $c\in \mathbb{N}$ be arbitrarily chosen.
4. Assume $(a,b)\in D\wedge (b,c)\in D$.
   1. $(a,b)\in D$ [Specialisation on line 4]
   2. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (a\cdot k=b)]$ [Definition of $D$]
   3. Let $t_1\in \mathbb{Z}$ such that $(t_1\ne 0)\wedge (a\cdot t_1=b)$. [Existential instantiation on line 4.2]
   4. $(b,c)\in D$ [Specialisation on line 4]
   5. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (b\cdot k=c)]$ [Definition of $D$]
   6. Let $t_2\in \mathbb{Z}$ such that $(t_2\ne 0)\wedge (b\cdot t_2=c)$. [Existential instantiation on line 4.5]
   7. $a\cdot t_1=b$ [Specialisation on line 4.3]
   8. $b\cdot t_2=c$ [Specialisation on line 4.6]
   9. $c=b\cdot t_2=a\cdot (t_1\cdot t_2)$ [Basic algebra]
   10. $t_1\cdot t_2\in \mathbb{Z}$ [Basic algebra]
   11. $t_1\ne 0$ [Specialisation on line 4.3]
   12. $t_2\ne 0$ [Specialisation on line 4.6]
   13. $t_1\cdot t_2\ne 0$ [Basic algebra]
   14. $(t_1\cdot t_2\ne 0)\wedge (a\cdot (t_1\cdot t_2)=c)$
   15. $\exists k\in \mathbb{Z}[(k\ne 0)\wedge (a\cdot k=c)]$ [Existential generalisation on line 4.10]
   16. $(a,c)\in D$ [Definition of $D$]
5. $((a,b)\in D\wedge (b,c)\in D)\to (a,c)\in D$ [Implication introduction on lines 4 and 4.10]
6. $\forall c\in \mathbb{N}\left[\right((a,b)\in D\wedge (b,c)\in D)\to (a,c)\in D]$ [Universal generalisation on lines 3 and 5]
7. $\forall b\in \mathbb{N},\forall c\in \mathbb{N}\left[\right((a,b)\in D\wedge (b,c)\in D)\to (a,c)\in D]$ [Universal generalisation on lines 2 and 6]
8. $\forall a\in \mathbb{N},\forall b\in \mathbb{N},\forall c\in \mathbb{N}\left[\right((a,b)\in D\wedge (b,c)\in D)\to (a,c)\in D]$ [Universal generalisation on 1 and 7]

Congruence is transitive

Theorem

Let $C_n=\{(a,b)\in \mathbb{Z}\times \mathbb{Z}:\exists t\in \mathbb{Z}[a-b=n\cdot k]\}$.

Then $C_n$ is transitive.

Proof

1. Let $a\in \mathbb{Z}$ be arbitrarily chosen.
2. Let $b\in \mathbb{Z}$ be arbitrarily chosen.
3. Let $c\in \mathbb{Z}$ be arbitrarily chosen.
4. Assume $(a,b)\in C_n\wedge (b,c)\in C_n$.
   1. $(a,b)\in C_n$ [Specialisation on line 4]
   2. $\exists k\in \mathbb{Z}[a-b=n\cdot k]$ [Definition of $C_n$]
   3. Let $t_1\in \mathbb{Z}$ such that $a-b=n\cdot t_1$. [Existential instantiation on line 4.2]
   4. $(b,c)\in C_n$ [Specialisation on line 4]
   5. $\exists k\in \mathbb{Z}[b-c=n\cdot k]$ [Definition of $C_n$]
   6. Let $t_2\in \mathbb{Z}$ such that $b-c=n\cdot t_2$. [Existential instantiation on line 4.2]
   7. $a-c=(a-b)+(b-c)=t_1\cdot n+t_2\cdot n=(t_1+t_2)\cdot n$ [Basic algebra]
   8. $t_1+t_2\in \mathbb{Z}$ [Basic algebra]
   9. $\exists k\in \mathbb{Z}[a-c=n\cdot k]$ [Existential generalisation on lines 4.7 and 4.8]
   10. $(a,c)\in C_n$ [Definition of $C_n$]
5. $((a,b)\in C_n\wedge (b,c)\in C_n)\to (a,c)\in C_n$ [Implication introduction on lines 4 and 4.10]
6. $\forall c\in \mathbb{Z}\left[\right((a,b)\in C_n\wedge (b,c)\in C_n)\to (a,c)\in C_n]$ [Universal generalisation on lines 3 and 5]
7. $\forall b\in \mathbb{Z},\forall c\in \mathbb{Z}\left[\right((a,b)\in C_n\wedge (b,c)\in C_n)\to (a,c)\in C_n]$ [Universal generalisation on lines 2 and 6]
8. $\forall a\in \mathbb{Z},\forall b\in \mathbb{Z},\forall c\in \mathbb{Z}\left[\right((a,b)\in C_n\wedge (b,c)\in C_n)\to (a,c)\in C_n]$ [Universal generalisation on lines 1 and 7]

In summary:

Here’s a table that summarises what we have proven about the two relations we’ve been using:

Relation	Reflexive?	Symmetric?	Anti-Symmetric?	Transitive?
Divisibility, $D$	Yes	No	Yes	Yes
Congruence modulo $n$	Yes	Yes	No	Yes

---

Bonus: Relations in Computer Science

The four properties we covered aren’t the only possible properties we care about for relations, but they are the main properties that everyone starts with.

In distributed systems, you might see other properties that they care about, stuff like message and program ordering.

Here’s some example slides of relations being used in very high-level computer science:

• Message Ordering and Group Communication
• Declarative Semantics for Concurrency