Unit 2: Introduction to Sets, Notations and Operations

This unit introduces the notion of sets and set operations. The unit will introduce:

1. Motivation for this unit
2. Basic sets, creating sets, set operations
3. Ways to prove set equivalence
4. More proofs with sets

---

Part 0: Unit Introduction

Recall that in this section on quantifiers we had this spiffy diagram that explained how you should read quantified statements.

And throughout Unit 1 itself we had slowly introduced more and more common sets that mathematicians use. Here’s a nice table that summarises the ones we have seen so far:

Symbol	Definition	Explanation
$\mathbb{N}$	Set of natural numbers	Set containing the numbers $0,1,2,3,\dots$
$\mathbb{Z}$	Set of integers	Set containing the numbers $\dots ,-3,-2,-1,0,1,2,3,\dots$
$\mathbb{Q}$	Set of rational numbers	Set containing numbers that can be expressed as a fraction of two integers, e.g., $0.33\bar{3}=\frac{1}{3}$ and $-20=\frac{40}{-2}$

In this unit, we will delve into this a little deeper. Concepts used here, and in the next unit on relations are useful for concepts like databases and distributed systems. In a nutshell, sets and relations are also part of the lingo (or vocabulary) on how we communicate. Let me show you a few examples to motivate this. At the end of this unit on sets, some of these examples should hopefully be a little more readable.

Motivation 1: Algorithms

For example, let’s say you’re reading a new book on algorithms, and it says the following:

An array $arr=a_1,a_2,\dots ,a_n$ of $n$ elements from $\mathbb{Z}$ is called sorted if $\forall i\in [n],\forall j\in [i][a_j\le a_i]$

How do we read this? From the previous unit, we might get some idea. For example, looking at the notation "$\forall i\in [n]$", we probably get that this means variable $i$ was taken from some set $[n]$, but what is set $[n]$? Similarly, variable $j$ was taken from set $[i]$. What is set $[i]$? That’s one thing this unit will show you.

Motivation 2: Databases

Later on (beyond this module) you might learn about databases. Databases are a tool to help you manage data. Here’s an oversimplification of some of the concepts (you will get to delve deeper when you take the module):

Let’s say we have two tables of data (don’t worry about what a table is, you can pretend they’re like Microsoft Excel spreadsheets):

Table 1:

Name	Email
Jon Snow	jsnow@gmail.com
Barry Allen	the_flash@hotmail.com
Pikachu	pika@pokemail.com

Table 2:

Name	Email
Matt Murdock	dared@gmail.com
Bruce Wayne	batman@waynemail.com
Barry Allen	the_flash@hotmail.com

Using these two sheets, let’s say we were told to merge them into a single table with all the data from both initial tables. So something like:

Resulting table:

Name	Email
Matt Murdock	dared@gmail.com
Bruce Wayne	batman@waynemail.com
Barry Allen	the_flash@hotmail.com
Jon Snow	jsnow@gmail.com
Pikachu	pika@pokemail.com

Notice here Barry Allen was in both tables and is a duplicate, but this table contains a combination of both original tables.

But there are other possible operations we could perform. What if our boss on the other hand wanted us to create a new table, that only has the common rows of the first 2 tables? Then our output table should be:

Resulting table:

Name	Email
Barry Allen	the_flash@hotmail.com

Because Barry Allen with that email is the only common entry in both tables.

These are examples of operations we can perform on data. In discrete math, the starting point for learning how to do this is via set operations. This is also another thing we will cover in this chapter.

As we get more and more involved, we will see how we can analyse more complex set operations as well.

Motivation 3: ML and AI

Lastly, coming back to the theme and goal of understanding math text and exposition, it’s very common that high-level concepts (especially algorithms) commonly use set notation and concepts related to sets. To understand these in the later module, knowing how to read even more symbols is quite useful. For example, later in the semester when we talk about graphs and trees, we will be using sets. Graphs are also useful when talking about stuff like decision trees or neural nets for AI, and so on.

In conclusion, think of this as yet another part of the vocabulary that will be useful further down the road. This is not to say that this isn’t useful by itself, but perhaps the more application-oriented among you might want to look ahead and understand that this topic has uses down the road.

---

Part 1: Basic Sets, Creating Sets, Set Operations

Basic Set Notations

Set-roster notation

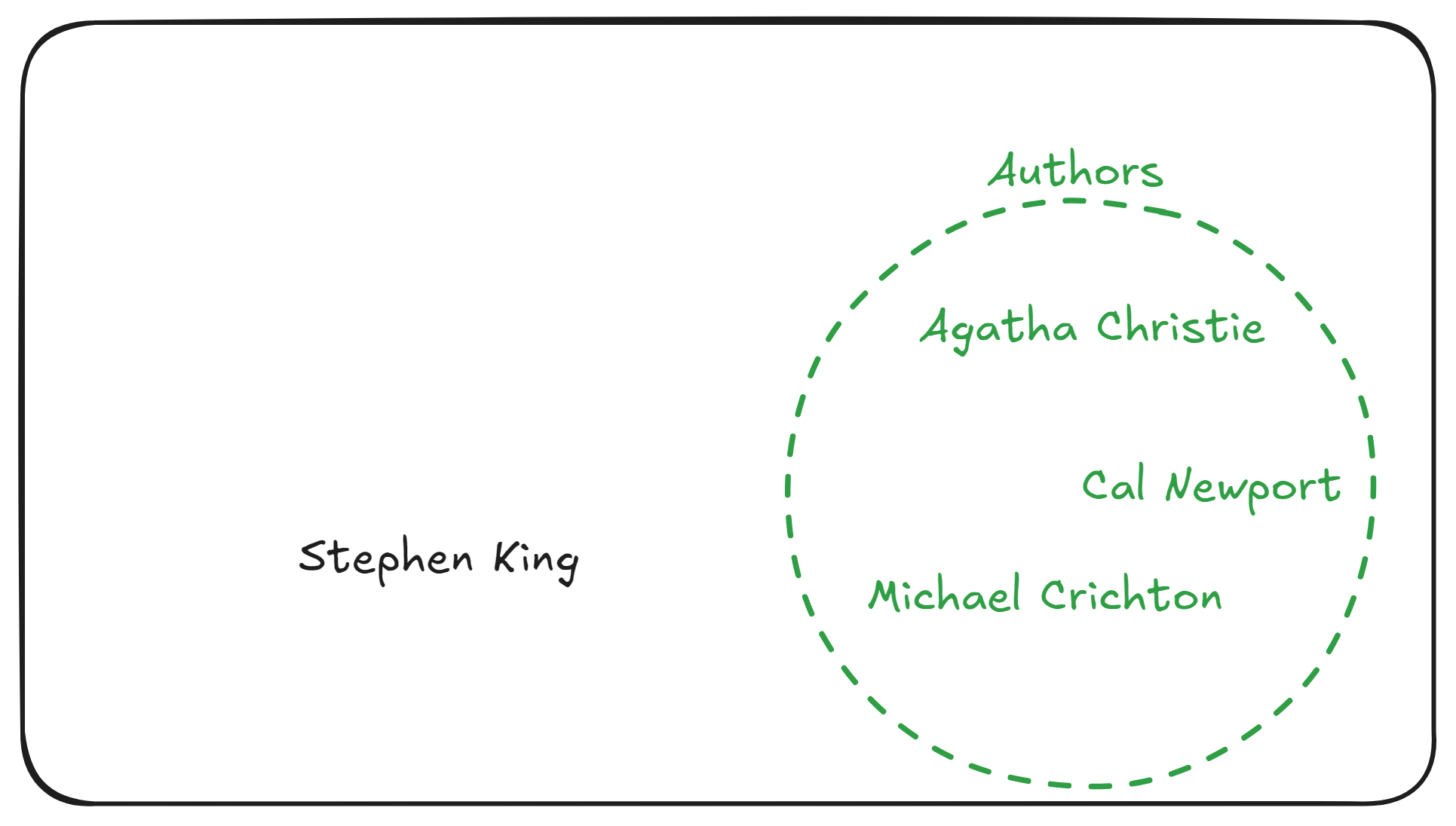
Let’s begin by talking about what a set is—a set is just a collection of objects. So for example, let’s say we wanted to represent the collection of someone’s favourite authors, we could write something like:

$$A=\{\text{Agatha Christie},\text{Cal Newport},\text{Michael Crichton}\}$$

Here, we are saying set $A$ contains $3$ objects, namely: $\text{Agatha Christie}$, $\text{Cal Newport}$ and $\text{Michael Crichton}$.

Pay attention to how we are using the "$\{$" symbol to start the set, and the "$\}$" symbol to end the set. We also use the "$,$" symbol to separate elements of the set.

So if we want to create sets by listing out the elements one by one, that is what we call set-roster notation. Here are a few more examples:

Example

Let $B$ be the set that contains the first three prime numbers, then:

$$B=\{2,3,5\}$$

Example

Let $C$ be the set that contains the integers $1,50,241,1234,9501234$, then:

$$C=\{1,50,241,1234,9501234\}$$

Set-roster notation can be a little boring at times since we really have to hand-write all the elements.

Element of

Using the same set again:

$$A=\{\text{Agatha Christie},\text{Cal Newport},\text{Michael Crichton}\}$$

We say $\text{Agatha Christie}$ is an element of set $A$. You might remember, we write this as $\text{Agatha Christie}\in A$. The "$\in$" symbol here means “is an element of”. Similarly, this means we can also say $\text{Cal Newport}\in A$, and also $\text{Michael Crichton}\in A$.

Let’s say we had some other author: $\text{Stephen King}$, and notice here he’s not in set $A$. We can write this in one of two ways, they’re both the same:

$$\text{Stephen King}\notin A$$

or,

$$\neg (\text{Stephen King}\in A)$$

Subset

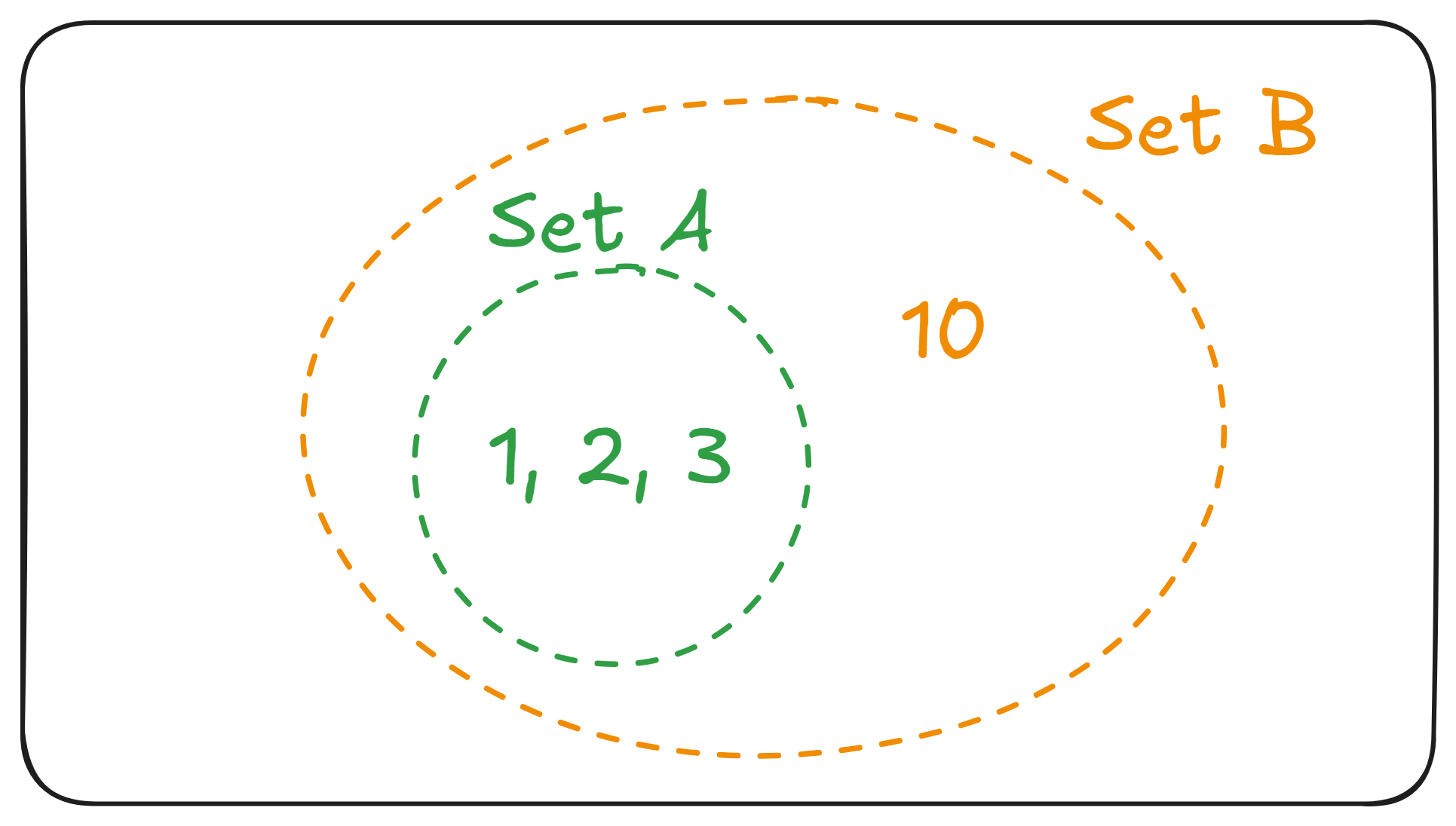
What happens if we have two sets, something like $A=\{1,2,3\}$ and $B=\{1,2,3,10\}$, then we want to be able to say:

Every object in $A$ is also an object in $B$.

Or, formally:

Definition: Subsets

Let $A$ be a subset of $B$, then: $\forall x\in A[x\in B]$ The symbol for this is $\subseteq$. So we would write $A\subseteq B$.

What about if we had a set $C=\{1,2\}$. Can we say that everything in $A$ is also in $C$? No we can’t. In particular, $3\in A$ but $3\notin C$. So in fact, we can say:

$$\exists x\in A[x\notin C]$$

which we know can be re-written:

$$\exists x\in A[x\notin C]\equiv \exists x\in A[\neg (x\in C)]\equiv \neg (\forall x\in A[x\in C])$$

Which confirms $\neg (A\subseteq C)$. As a shorthand, we can also write this as $A⊈C$.

Example

Let $A=\{2,4,6,8\}$, $B=\{2,4,6\}$. Then $A⊈B$ but $B\subseteq A$.

Example

Let $A=\{1,2,3,4\}$, $B=\{2,4,6,8\}$. Then $A⊈B$ and also $B⊈A$.

Empty sets

What about if we wanted a set that has no elements? There’s two ways we can write this. Though uncommon, some people might write it like so:

$$\{\}$$

The more common notation, and one you should get used to, is this:

$$\varnothing$$

Another also common way of writing it is like this:

$$\varnothing$$

The empty set is so that nothing is ever in the empty set, i.e., for any set $A$, we have $\forall x\in A[x\notin \varnothing ]$.

One important thing to note is that the empty set is always a subset of any other set. For example, $\varnothing \subseteq \{1,2\}$. It’s also a subset of itself! $\varnothing \subseteq \varnothing$.

Common sets of numbers

Let’s start talking about a few well-established symbols for sets. The most common are: $\mathbb{N},\mathbb{Z},\mathbb{Q},\mathbb{R}$, and $\mathbb{C}$.

Symbol	Definition	Explanation
$\mathbb{N}$	Set of natural numbers	Set containing the numbers $0,1,2,3,\dots$
$\mathbb{Z}$	Set of integers	Set containing the numbers $\dots ,-3,-2,-1,0,1,2,3,\dots$
$\mathbb{Q}$	Set of rational numbers	Set containing numbers that can be expressed as a fraction of 2 integers, e.g., $0.33\bar{3}=\frac{1}{3}$ and $-20=\frac{40}{-2}$
$\mathbb{R}$	Set of real numbers	Set containing any number that is not complex
$\mathbb{C}$	Set of imaginary/complex numbers	For example, something like $i$, or $-i$ is complex but not real

There is one more common notation that we use in computer science. It turns out for some natural number $n$, it’s very convenient for us to think about the set $\{1,\dots ,n\}$. The notation for this is $[n]$.

Example

$$[5]=\{1,2,3,4,5\}$$

Example

$$[1]=\{1\}$$

Example

$$[0]=\varnothing$$

Explanation: There are no numbers that start from $1$ and end at $0$ ($\ge 1$ and $\le 0$).

Set-builder notation

Okay, well right now we’ve seen a bunch of sets, but we haven’t really built or made anything too big. If we wanted some kind of special, custom set, we’ve had to manually list out all the elements. What if we wanted the set of even numbers? We can’t just write everything out one by one… that would take forever!

Here’s how we would do it:

$$A=\{x\in \mathbb{Z}:\exists k\in \mathbb{Z}[x=2k]\}$$

Let’s read this back:

$A$ is a set that contains any element $x$ from $\mathbb{Z}$, such that, the following statement about $x$ holds true: $\exists k\in \mathbb{Z}[x=2k]$

Let’s see how this works. Consider a number like $18$. Is $18\in A$? Well, does it satisfy the statement? $18=2\cdot 9$ and $9\in \mathbb{Z}$. So there exists a $k\in \mathbb{Z}$ such that $18=2\cdot k$. So the condition holds! This means that $18\in A$.

What about something like $3$? Recall from this section, we proved that $\neg even(3)$, or in other words, $\neg (\exists k\in \mathbb{Z}[3=2k])$. So that means that $3$ does not fulfil the condition. So we can conclude that $3\notin A$.

Here are a few more examples:

Example

The set $A$ of real numbers between $5$ and $6$ (inclusive) can be written as:

$$A=\{x\in \mathbb{R}:5\le x\wedge x\le 6\}$$

For example, $5\in A$, $6\in A$, $5.5\in A$, and so on, but $4.9\notin A$.

Example

The set $C$ of real numbers between $1$ and $3$ (exclusive) can be written as:

$$C=\{x\in \mathbb{R}:1<x\wedge x<3\}$$

For example, $1\notin C$ and $3\notin C$, but $2\in C$, and since $\sqrt{2}\approx 1.414$, $\sqrt{2}\in C$.

Example

The set of natural numbers that divides $6$ can be written as:

$$D=\{x\in \mathbb{N}:\exists k\in \mathbb{N}[x\cdot k=6]\}$$

So $D=\{1,2,3,6\}$. Why is $2\in D$? Because we can find a $k\in \mathbb{N}$ such that $2\cdot k=6$. In particular, $3\in \mathbb{N}$ and is such that $2\cdot 3=6$.

A similar reasoning applies for the rest of the elements.

Example

The set of prime numbers can be written as:

$B=\{x\in \mathbb{N}:x\ge 2\wedge (\forall d\in \mathbb{N}[divides(d,x)\to (d=1\vee d=x)]\left)\right\}$

where the predicate $divides(d,x)$ is defined as $\exists k\in \mathbb{Z}[d\cdot k=x]$.

Again, for example, is $7\in B$? We know $7$ only has two divisors: $1$ and $7$ itself. So let’s check: $7$ is greater than or equal to $2$; take any $d\in \mathbb{N}$, if $d$ does in fact divide $7$, we know it has to be either $1$ or $7$. So we can conclude that $7$ is indeed in $B$.

On the other hand, something like $10$, has divisors $1$, $2$, $5$, $10$. $10$ is indeed greater than or equal to $2$. But what about the second half of the condition? Let’s see. Consider value $5$. $5$ is in $\mathbb{N}$, and $divides(5,10)$ is $true$. But $5$ is neither $1$ nor $10$. So $(5=1\vee 5=10)$ is $false$. This means the condition $(\forall d\in \mathbb{N}[divides(d,10)\to (d=1\vee d=10)])$ is $false$. So $10$ fails the condition, which means that $10\notin B$.

Set-builder notation is pretty handy, so let’s talk about the general format now:

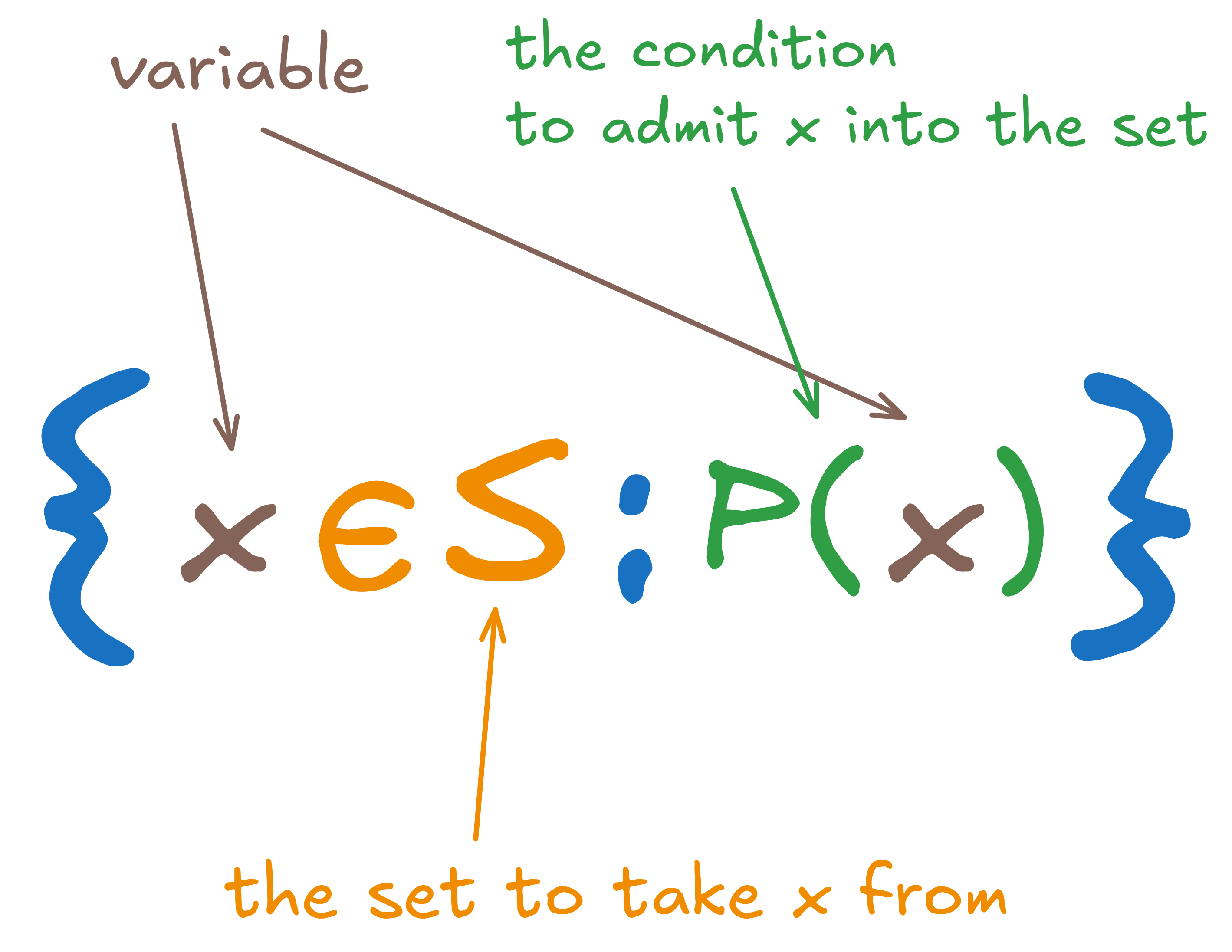
So again, we go through elements from some set $S$, and if it fulfils the conditions laid out by $P(x)$, we will admit element $x$ into set $S$.

Example

Let’s try one more example: let’s say we want the even integers between $1$ and $10$ inclusive. We could also write this:

$\{x\in [10]:\exists k\in \mathbb{Z}[x=2k]\}$

Pay special attention to how this time around we used $x\in [10]$, instead of $x\in \mathbb{Z}$ as before. There is an alternative way to write this:

$\{x\in \mathbb{Z}:x\ge 1\wedge x\le 10\wedge (\exists k\in \mathbb{Z}[x=2k])\}$

Set Operations

The next thing to do is to talk about the set operations. These are ways that we can build bigger sets from the ones we currently have. These are super handy and are part and parcel of database operations, and also they somewhat correspond to our logical operations, as we will see.

As a summary, these are almost all the set operations:

1. Set union
2. Set intersection
3. Set difference
4. Power set
5. Cartesian product

Set union

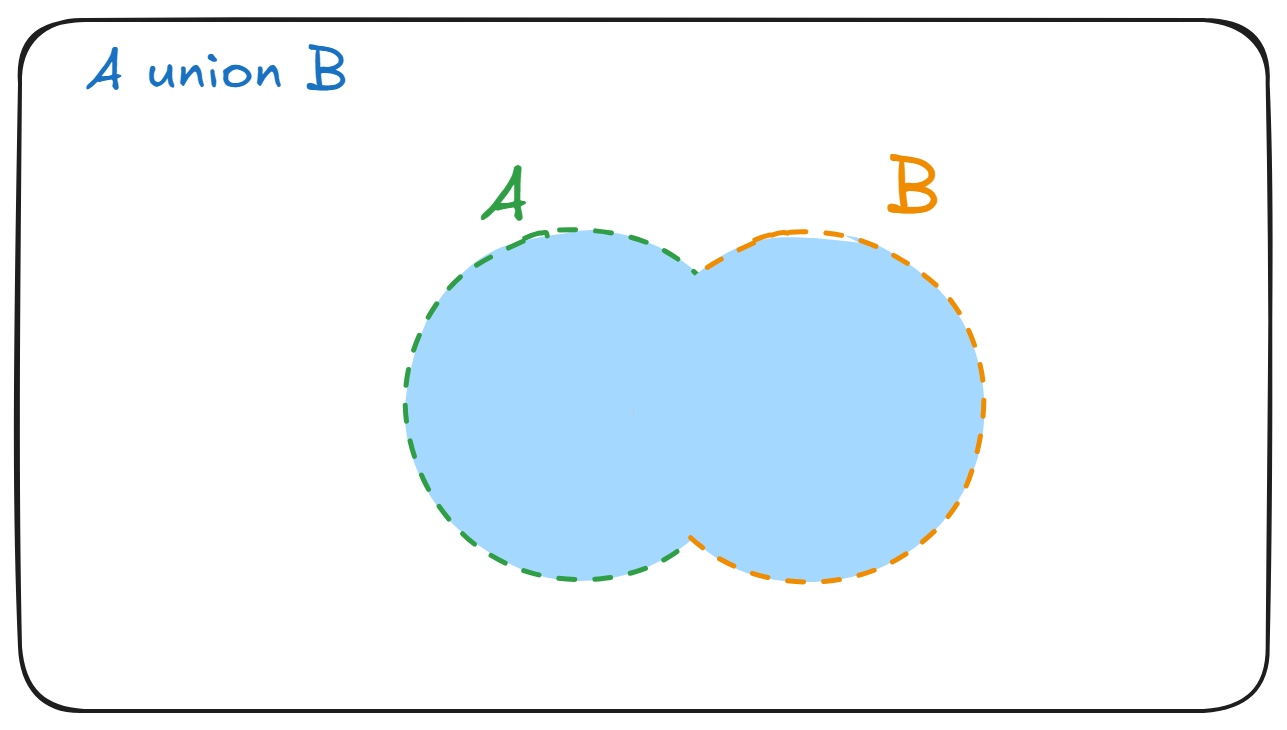
Given two sets $A$ and $B$, we can create a new set $C=A\cup B$, which is the union of $A$ and $B$. The set $C$ contains elements that are either in $A$ or in $B$.

Definition: Set union

The set union of $A$ and $B$, denoted $A\cup B$ is the set which contains all the elements of $A$ and $B$.

Formally, $A\cup B=\{x:(x\in A)\vee (x\in B)\}$

Example

$$\{1,2,3,4,5,7,8,9,10\}=\{1,2,3,4,5,10\}\cup \{1,7,8,9,10\}$$

Example

For example, we want to make a set $C$ that contains both positive odd numbers, and all negative numbers. Then we can do it in the following way:

$$C=\{x\in \mathbb{N}:\exists k\in \mathbb{Z}[x=2k+1]\}\cup \{x\in \mathbb{Z}:x\le -1\}$$

Example

For example, we want to make a set $C$ that contains both non-negative odd numbers, and also non-negative even numbers:

$$C=\{x\in \mathbb{N}:\exists k\in \mathbb{Z}[x=2k+1]\}\cup \{x\in \mathbb{N}:\exists k\in \mathbb{Z}[x=2k]\}$$

Wait a minute, isn’t this just $\mathbb{N}$?

Yes, yes it is!

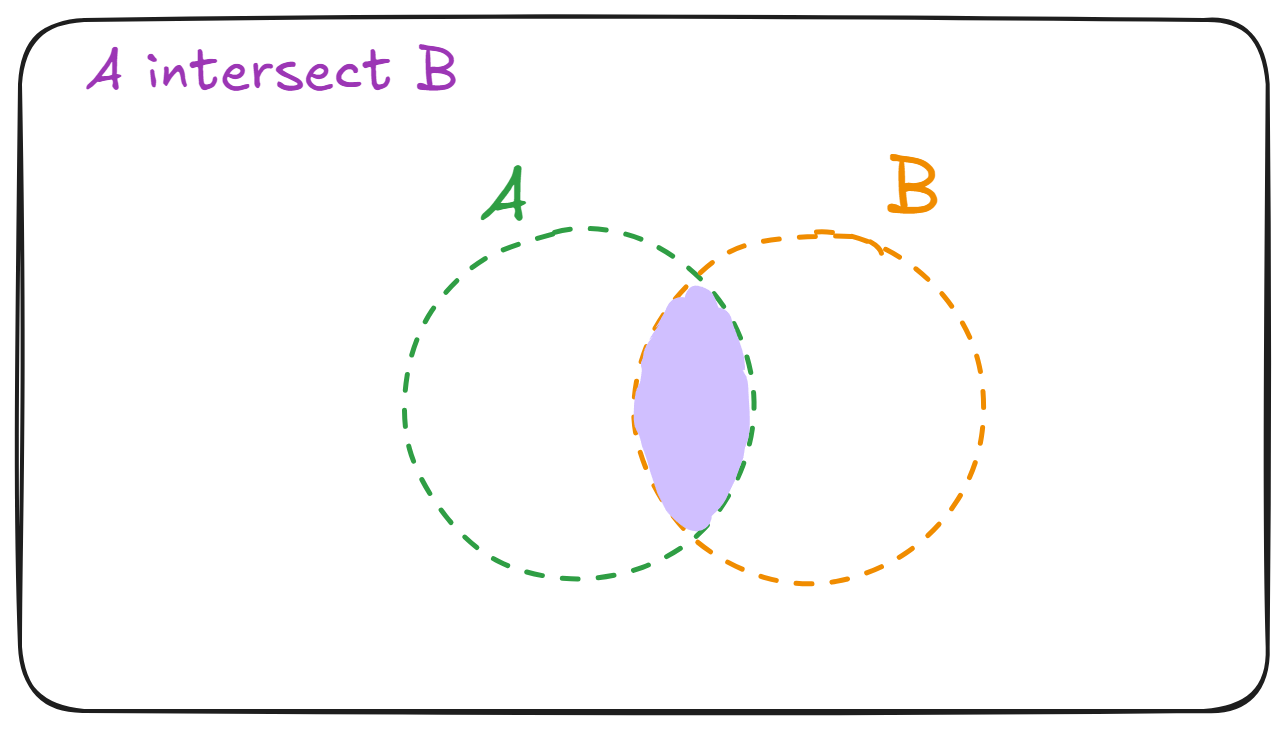
Set intersection

Given two sets $A$ and $B$, we can create a new set $C=A\cap B$ which is the intersection of $A$ and $B$. The set $C$ contains elements that are both in $A$ and in $B$.

Definition: Set intersection

The set intersection of $A$ and $B$, denoted $A\cap B$ is the set which contains all the common elements of $A$ and $B$.

Formally, $A\cap B=\{x:(x\in A)\wedge (x\in B)\}$

Example

$$\{1,3,10\}=\{1,2,3,4,5,10\}\cap \{1,7,8,9,10\}$$

Example

For example, we want to make a set $C$ that contains even numbers that are only negative. We could do so in the following way:

$$C=\{x\in \mathbb{Z}:\exists k\in \mathbb{Z}[x=2k]\}\cap \{x\in \mathbb{Z}:x\le -1\}$$

Example

$A=\{1,2\}$, $B=\{5\}$, then: $A\cap B=\varnothing$

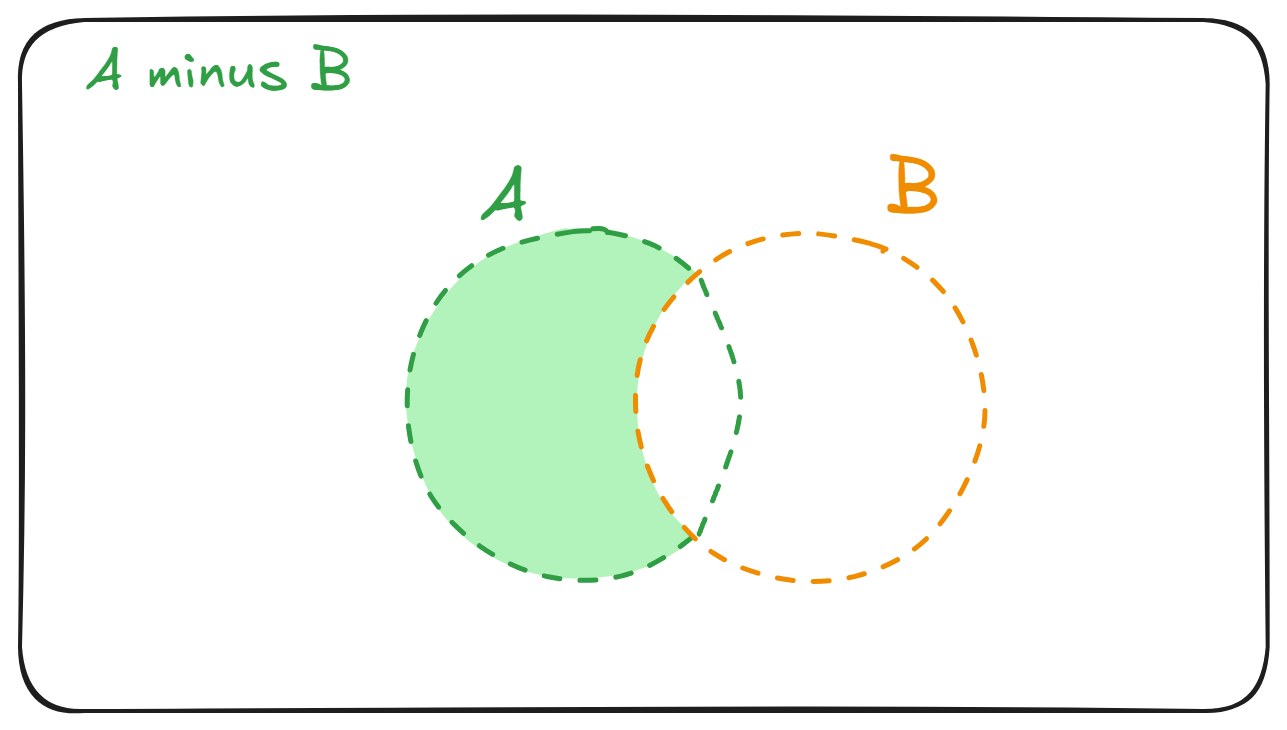
Set difference

Given two sets $A$ and $B$, we can create a new set $C=A\setminus B$, which we call $A$ minus $B$. The set $C$ contains elements that are from in $A$ that is not also in $B$.

Definition: Set difference

The set difference $A$ minus $B$, denoted $A\setminus B$, contains all the elements of $A$ that are not in $B$.

Formally, $A\setminus B=\{x\in A:x\notin B\}$

Example

Let $A=\{1,2,3,4,5,10\}$, and $B=\{1,7,8,9,10\}$.

$$\{2,3,4,5\}=\{1,2,3,4,5,10\}\setminus \{1,7,8,9,10\}$$

Notice that elements $1$ and $10$ are in $A$ but also in $B$, so it is not in $C=A\setminus B$. On the other hand, elements $2,3,4,5$ are in $A$ but not in $B$, so they are in $C$.

Also, note that the sets $A\setminus B$ and $B\setminus A$ are not the same sets! In this case, $B\setminus A$ would contain all the elements in $B$ that are not in $A$, which is the set $\{7,8,9\}$. Notice that this is not the same as $A\setminus B=\{2,3,4,5\}$.

Example

For example, we want to make a set $C$ that contains any non-negative number that is not prime. Then we can do the following:

Let $B=\{x\in \mathbb{N}:x\ge 2\wedge (\forall d\in \mathbb{N}[divides(d,x)\to (d=1\vee d=x)]\left)\right\}$ where the predicate $divides(d,x)$ is defined as $\exists k\in \mathbb{Z}[d\cdot k=x]$.

Then $C=\mathbb{N}\setminus B$.

Notice here $C$ contains any element from $\mathbb{N}$ that is not in set $B$ (which is the set of primes).

Power set

The power set operation is a little unorthodox, since it does not look like a logical operation like the ones we have seen. Given a set $A$, the power set of $A$ is denoted by $\mathcal{P}(A)$ is the set that contains all subsets of $A$.

Definition: Power set

The power set of $A$, denoted $\mathcal{P}(A)$, is the set containing all subsets of $A$.

Formally, $X\in \mathcal{P}(A)\leftrightarrow X\subseteq A$

In other words, if $X$ is a subset of $A$, then $X$ is in the power set of $A$ and if $X$ is in the power set of $A$, then $X$ is a subset of $A$.

Example

$\mathcal{P}(\{0,1\})=\{\varnothing ,\{0\},\{1\},\{0,1\}\}$

Notice here that: $\varnothing \subseteq \varnothing$, so $\varnothing \in \mathcal{P}(\varnothing )$.

Similarly, a set like $\{0\}\subseteq \{0,1\}$ so $\{0\}\in \mathcal{P}(\{0,1\})$.

Example

$\mathcal{P}(\varnothing )=\{\varnothing \}$

Remember, $\varnothing \subseteq \varnothing$, so $\varnothing \in \mathcal{P}(\varnothing )$.

$\subseteq$ vs. $\in$

Here, we make a clear distinction between being a subset and being an element of a set. Consider the set $A=\{1,2,3\}$. Then, the following statements are true:

• $3\in A$
• $\{3\}\in \mathcal{P}(A)$
• $\{3\}\subseteq A$

However, it is erroneous to say that $3\in \mathcal{P}(A)$, or that $\{3\}\in A$.

Cartesian product

Given two sets $A$ and $B$, the set $C=A\times B$ is the cartesian product between sets $A$ and $B$. This creates pairs. If $x\in A$ and $y\in B$, then the pair $(x,y)\in C$.

Definition: Cartesian product

The Cartesian product of two sets $A$ and $B$, denoted $A\times B$, contains all pairs $(x,y)$ whose first element $x$ is from $A$ and whose second element $y$ is from $B$.

Formally, $A\times B=\{(x,y):(x\in A)\wedge (y\in B)\}$

Therefore, $(x,y)\in A\times B\leftrightarrow (x\in A)\wedge (y\in B)$ and $(x,y)\notin A\times B\leftrightarrow (x\notin A)\vee (y\notin B)$

Note: This operation is one of the most important ones, enabling us to create many other mathematical objects later on (e.g., relations, graphs).

Example

Let $A=\{1,2,3\}$ and $B=\{1,2\}$.

$$A\times B=\{(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)\}$$

Pictorially, you can see how we got the elements.

Notice here the pairs are ordered. So $(1,2)\in A\times B$, and $(2,1)\in A\times B$. But $(1,2)\ne (2,1)$. Also, $(1,3)\notin A\times B$.

Example

$\mathbb{Z}\times \mathbb{Z}$ is the set that contains any pair of integers. For example, $(-1,25)\in \mathbb{Z}\times \mathbb{Z}$. But $(\frac{1}{2},21)\notin \mathbb{Z}\times \mathbb{Z}$.

Example

$\mathbb{Q}\times \mathbb{Z}$ is the set that contains any pair where the first element is from $\mathbb{Q}$ and the second is from $\mathbb{Z}$. For example, $(-1,25)\in \mathbb{Q}\times \mathbb{Z}$, and also $(\frac{1}{2},21)\in \mathbb{Q}\times \mathbb{Z}$.

---

Part 2: Ways to Prove Set Equivalence

Up until this point, we have been showing how to manipulate and create all kinds of sets. And you might have noticed, that sometimes there’s more than one way to create a set. Also, knowing when two sets are equivalent is pretty helpful for something like databases (for those who are curious and would like a sneak peek, you might look want to take a peek at the concepts relational algebra, and relational calculus for databases).

We say that two sets $A$ and $B$ are equivalent or equal if they have the same elements.

Definition: Set equivalence

Two sets $A$ and $B$ are equivalent or equal if and only if every element in $A$ is in $B$ and every element in $B$ is also in $A$.

Formally, $A=B\leftrightarrow (\forall x\in A[x\in B])\wedge (\forall y\in B[y\in A])$

Equivalently, $A=B\leftrightarrow (A\subseteq B)\wedge (B\subseteq A)$

There’s broadly two categories for how to show two sets are equivalent. We will be showing both ways.

Method 1: Directly proving two sets are subsets of each other

Consider the following set:

$$A=\{x\in \mathbb{N}:odd(x)\}$$

which is the set of odd natural numbers. But what if we wrote it like this?

$$B=\mathbb{N}\setminus \{x\in \mathbb{N}:even(x)\}$$

which is the set of natural numbers that are not even. These two are intuitively the same set right? Let’s see a proof of this. We’ll use these two lemmas:

Lemmas

1. $\forall x\in \mathbb{N}[\neg even(x)\to odd(x)]$
2. $\forall x\in \mathbb{N}[odd(x)\to \neg even(x)]$

where $even(x)\equiv \exists k\in \mathbb{N}[x=2k]$ and $odd(x)\equiv \exists k\in \mathbb{N}[x=2k+1]$.

In English, the first statement is saying “Every natural number is such that if it is not even, it is odd.” The second statement is saying “Every natural number that is odd is not even.”

Okay, so we’ve established those lemmas, let’s see how to prove the two sets are the same. Our goal is to show the statement $A\subseteq B\wedge B\subseteq A$. How do we do this? Remember that $A\subseteq B$ is defined to be $\forall x\in A[x\in B]$. So we effectively want to prove:

$$(\forall x\in A[x\in B])\wedge (\forall x\in B[x\in A])$$

And remember the definitions of the sets $A$ and $B$:

$$A=\{x\in \mathbb{N}:odd(x)\}$$ $$B=\mathbb{N}\setminus \{x\in \mathbb{N}:even(x)\}$$

Proof

1. Let $y\in A$ be arbitrarily chosen.
   1. $y\in \mathbb{N}\wedge odd(y)$ [Definition of $A$]
   2. $odd(y)$ [Specialisation on line 1.1]
   3. $y\in \mathbb{N}$ [Specialisation on line 1.1]
   4. $\forall x\in \mathbb{N}[odd(x)\to \neg (even(x))]$ [Lemma 2]
   5. $odd(y)\to \neg (even(y))$ [Universal instantiation on lines 1.3 and 1.4]
   6. $\neg (even(y))$ [Modus ponens on lines 1.2 and 1.5]
   7. $y\in \mathbb{N}\wedge \neg (even(y))$ [Conjunction on lines 1.3 and 1.6]
   8. $\neg (y\in \{x\in \mathbb{N}:even(x)\})$ [Definition based on set-builder]
   9. $y\in \mathbb{N}\wedge \neg (y\in \{x\in \mathbb{N}:even(x)\})$ [Conjunction on lines 1.3 and 1.8]
   10. $y\in B$ [Definition of $B$ and set difference]
   11. $\forall y\in A[y\in B]$ [Universal generalisation on lines 1 and 1.10]
2. Let $z\in B$ be arbitrarily chosen.
   1. $z\in \mathbb{N}\wedge \neg (z\in \{x\in \mathbb{N}:even(x)\})$ [Definition of $B$]
   2. $z\in \mathbb{N}$ [Specialisation on line 2.1]
   3. $\neg (z\in \{x\in \mathbb{N}:even(x)\})$ [Specialisation on line 2.1]
   4. $z\notin \mathbb{N}\vee \neg (even(z))$ [Definition based on set-builder]
   5. $z\in \mathbb{N}\to \neg (even(z))$ [Logically equivalent to line 2.4 (Why?)]
   6. $\neg (even(z))$ [Modus ponens on lines 2.2 and 2.5]
   7. $\forall x\in \mathbb{N}[\neg (even(x))\to odd(x)]$ [Lemma 1]
   8. $\neg (even(z))\to odd(z)$ [Universal instantiation on lines 2.2 and 2.7]
   9. $odd(z)$ [Modus ponens on lines 2.6 and 2.8]
   10. $z\in \mathbb{N}\wedge odd(z)$ [Conjunction on lines 2.2 and 2.9]
   11. $z\in A$ [Definition of $A$]
   12. $\forall z\in B[z\in A]$ [Universal generalisation on lines 2 and 2.11]
3. $(\forall y\in A[y\in B])\wedge (\forall z\in B[z\in A])$ [Conjunction on lines 1.11 and 2.12]
4. $A=B$. [Definition of set equivalence]

Why is line 2.5 valid?

The step from line 2.4 to line 2.5 corresponds to the following equivalence: $p\to q\equiv \neg p\vee q$ where $p\equiv z\in \mathbb{N}$ and $q\equiv \neg (even(z))$. Try convincing yourself that this equivalence is true!

And we’ve proven they’re the same set! So again, the takeaway is the following:

To prove two sets $A$ and $B$ have the same elements, we should prove $A\subseteq B\wedge B\subseteq A$. Or in other words:

$$(\forall x\in A[x\in B])\wedge (\forall x\in B[x\in A])$$

Example

Let $A,B,C$ be any 3 sets. Then: $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

Here’s the proof:

Proof

1. Let $x\in A\cup (B\cap C)$ be arbitrarily chosen.
   1. $(x\in A)\vee (x\in B\cap C)$ [Definition of set union]
   2. Case 1: $x\in A$.
      1. $x\in A\vee x\in B$ [Generalisation on line 1.2]
      2. $x\in (A\cup B)$ [Definition of set union]
      3. $x\in A\vee x\in C$ [Generalisation on line 1.2]
      4. $x\in (A\cup C)$ [Definition of set union]
      5. $x\in (A\cup B)\wedge x\in (A\cup C)$ [Conjunction of lines 1.2.2 and 1.2.4]
      6. $x\in (A\cup B)\cap (A\cup C)$ [Definition of set intersection]
   3. Case 2: $x\in B\cap C$.
      1. $x\in B\wedge x\in C$ [Definition of set intersection]
      2. $x\in B$ [Specialisation on line 1.3.1]
      3. $x\in A\vee x\in B$ [Generalisation on line 1.3.2]
      4. $x\in (A\cup B)$ [Definition of set union]
      5. $x\in C$ [Specialisation on line 1.3.1]
      6. $x\in A\vee x\in C$ [Generalisation on line 1.3.5]
      7. $x\in (A\cup C)$ [Definition of set union]
      8. $x\in (A\cup B)\wedge x\in (A\cup C)$ [Conjunction on lines 1.3.4 and 1.3.7]
      9. $x\in (A\cup B)\cap (A\cup C)$ [Definition of set intersection]
   4. In all cases, it is shown that $x\in (A\cup B)\cap (A\cup C)$ [Proof by cases on lines 1.1, 1.2.6, 1.3.9]
   5. $\forall x\in A\cup (B\cap C)[x\in (A\cup B)\cap (A\cup C)]$ [Universal generalisation on lines 1 and 1.4]
2. Let $x\in (A\cup B)\cap (A\cup C)$ be arbitrarily chosen.
   1. $x\in (A\cup B)\wedge x\in (A\cup C)$ [Definition of set intersection]
   2. $x\in (A\cup B)$ [Specialisation on line 2.1]
   3. $x\in A\vee x\in B$ [Definition of set union]
   4. $x\notin A\to x\in B$ [Logically equivalent to line 2.3 (Why?)]
   5. $x\in (A\cup C)$ [Specialisation on line 2.1]
   6. $x\in A\vee x\in C$ [Definition of set union]
   7. $x\notin A\to x\in C$ [Logically equivalent to line 2.6]
   8. Suppose $x\notin A$.
      1. $x\in B$ [Modus ponens on lines 2.4 and 2.8]
      2. $x\in C$ [Modus ponens on lines 2.7 and 2.8]
      3. $x\in B\wedge x\in C$ [Conjunction on lines 2.8.1 and 2.8.2]
      4. $x\in (B\cap C)$ [Definition of set intersection]
   9. $x\notin A\to x\in (B\cap C)$ [Implication introduction on lines 2.8, 2.8.4]
   10. $x\in A\vee x\in (B\cap C)$ [Logically equivalent to line 2.10]
   11. $x\in A\cup (B\cap C)$ [Definition of set union]
   12. $\forall x\in (A\cup B)\cap (A\cup C)[x\in A\cup (B\cap C)]$ [Universal generalisation on lines 2, 2.11]
3. $\forall x\in A\cup (B\cap C)[x\in (A\cup B)\cap (A\cup C)]\wedge \forall x\in (A\cup B)\cap (A\cup C)[x\in A\cup (B\cap C)]$ [Conjunction on lines 1.5, 2.12]
4. $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$ [Definition of set equivalence]

Here’s another small example of two sets you can try to prove are the same.

Example

$A=\{x\in \mathbb{N}:x\le 5\vee x\ge 10\}$, $B=\{x\in \mathbb{N}:x\le 5\}$, and $C=\{x\in \mathbb{N}:x\ge 10\}$.

Then: $A=B\cup C$

Proof

1. Let $x\in A$ be arbitrarily chosen.
   1. $(x\in \mathbb{N})\wedge (x\le 5\vee x\ge 10)$ [Definition of $A$]
   2. $x\in \mathbb{N}$ [Specialisation on line 1.1]
   3. $x\le 5\vee x\ge 10$ [Specialisation on line 1.1]
   4. Case 1: $x\le 5$.
      1. $x\in \mathbb{N}\wedge x\le 5$ [Conjunction on lines 1.2 and 1.4]
      2. $x\in B$ [Definition of $B$]
      3. $x\in B\vee x\in C$ [Generalisation on line 1.4.2]
      4. $x\in B\cup C$ [Definition of set union]
   5. Case 2: $x\ge 10$.
      1. $x\in \mathbb{N}\wedge x\ge 10$ [Conjunction on lines 1.2 and 1.5]
      2. $x\in C$ [Definition of $C$]
      3. $x\in B\vee x\in C$ [Generalisation on line 1.5.2]
      4. $x\in B\cup C$ [Definition of set union]
   6. In all cases, we have $x\in B\cup C$. [Proof by cases on lines 1.3, 1.4.4, 1.5.4]
   7. $\forall x\in A[x\in B\cup C]$ [Universal generalisation on lines 1 and 1.6]
2. Let $y\in B\cup C$ be arbitrarily chosen.
   1. $y\in B\vee y\in C$ [Definition of set union]
   2. Case 1: $y\in B$.
      1. $y\in \mathbb{N}\wedge y\le 5$ [Definition of $B$]
      2. $y\in \mathbb{N}$ [Specialisation on line 2.2.1]
      3. $y\le 5$ [Specialisation on line 2.2.1]
      4. $y\le 5\vee y\ge 10$ [Generalisation on line 2.2.3]
      5. $y\in \mathbb{N}\wedge (y\le 5\vee y\ge 10)$ [Conjunction on lines 2.2.2 and 2.2.4]
      6. $y\in A$ [Definition of $A$]
   3. Case 2: $y\in C$.
      1. $y\in \mathbb{N}\wedge y\ge 10$ [Definition of $C$]
      2. $y\in \mathbb{N}$ [Specialisation on line 2.3.1]
      3. $y\ge 10$ [Specialisation on line 2.3.1]
      4. $y\le 5\vee y\ge 10$ [Generalisation on line 2.3.3]
      5. $y\in \mathbb{N}\wedge (y\le 5\vee y\ge 10)$ [Conjunction on lines 2.3.2 and 2.3.4]
      6. $y\in A$ [Definition of $A$]
   4. In all cases, we have $y\in A$. [Proof by cases on lines 2.1, 2.2.6, 2.3.6]
   5. $\forall y\in B\cup C[x\in A]$ [Universal generalisation on lines 2 and 2.4]
3. $(\forall x\in A[x\in B\cup C])\wedge (\forall y\in B\cup C[y\in A])$ [Conjunction on lines 1.7 and 2.5]
4. $A=B\cup C$. [Definition of set equivalence]

Method 2: Based on logical equivalences

You might have noticed that the set operations we are doing bear some similarity to the logical operations. For example, a set intersection ($\cap$) operation really does look a little bit like the logical and ($\wedge$) operation. After all, if $C=A\cap B$, then $C$ contains all elements $x$ such that $x\in A\wedge x\in B$. Similarly, if $D=A\cup B$, then $D$ contains all elements $x$ such that $x\in A\vee x\in B$.

What about the set difference ($\setminus$) operation? If $E=A\setminus B$, then $E$ contains all elements such that $x\in A\wedge x\notin B$, in other words: $x\in A\wedge \neg (x\in B)$.

Set operation	Logical operation
$A\cup B$	$a\vee b$
$A\cap B$	$a\wedge b$
$A\setminus B$	$a\wedge \neg b$

You might actually have noticed this based on the previous sub-section, when we proved the following:

$$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$$

You might have noticed it mirrors this fact:

$$x\in A\vee (x\in B\wedge x\in C)\equiv (x\in A\vee x\in B)\wedge (x\in A\vee x\in C)$$

This is actually something we can do in general. Hence, for the narrower use-cases of involving only intersections, set minus and union in very specific ways, here are some examples:

1. $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$
2. $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$
3. $A\setminus (B\cup C)=(A\setminus B)\cap (A\setminus C)$
4. $A\setminus (B\cap C)=(A\setminus B)\cup (A\setminus C)$

Why? They mirror how the following pairs of propositions are logically equivalent:

1. $a\vee (b\wedge c)\equiv (a\vee b)\wedge (a\vee c)$
2. $a\wedge (b\vee c)\equiv (a\wedge b)\vee (a\wedge c)$
3. $a\wedge \neg (b\vee c)\equiv a\wedge (\neg b\wedge \neg c)\equiv (a\wedge \neg b)\wedge (a\wedge \neg c)$
4. $a\wedge \neg (b\wedge c)\equiv a\wedge (\neg b\vee \neg c)\equiv (a\wedge \neg b)\vee (a\wedge \neg c)$

So what happens if someone asked you if something like whether these two sets are equal or not?

$$(A\cup B)\setminus C\stackrel{?}{=}(A\setminus C)\cup (B\setminus C)$$

Well, it’s the same as asking whether the following is logically equivalent:

$$(a\vee b)\wedge \neg c\stackrel{?}{\equiv }(a\wedge \neg c)\vee (b\wedge \neg c)$$

You can check that it is, and thus they are indeed the same set.

What about this?

$$(A\setminus B)\setminus C\stackrel{?}{\equiv }A\setminus (B\setminus C)$$

We are basically checking whether this is equivalent:

$$(a\wedge \neg b)\wedge \neg c\stackrel{?}{\equiv }a\wedge \neg (b\wedge \neg c)$$

You might realise, they’re not. In fact, in terms of the proposition, if we set $a\equiv true$, $b\equiv true$, $c\equiv true$, then the left hand side is $false$, but the right hand side is $true$.

But what about the sets? The fact that we found a way to show the propositions were not logically equivalent gives us a hint. Let’s try something like $A=\{1\},B=\{1\},C=\{1\}$.

Then $(A\setminus B)\setminus C=\varnothing$, but $A\setminus (B\setminus C)=\{1\}$. Try it step by step to check that what we’ve written here is correct!

This method however, is less general—it typically does not work if we involve sets that use set-builder notation to construct.

---

Part 3: More Proofs With Sets

Now that we have seen a few ideas about sets. We will end this unit on a few more commonly proven concepts about sets. Thus far we’ve only talked about set equivalences, unions and intersections. Let’s explore a few more ideas that have to do with the power set and cartesian product operations.

Reasoning About Subsets

Here are a example few intuitive facts we can prove involving subsets:

1. If $A$ is a subset of $B$ and $B$ is a subset of $C$, then $A$ is a subset of $C$.
2. If $A,B$ are subsets of $C$, then $A\cup B$ is a subset of $C$.
3. $A\cap B$ is a subset of $A$.

The key takeaway here are not the facts themselves. Rather, notice our approach has a common theme: We start with an element that is from the “smaller” set, and we show it is in the bigger set.

Example

$(A\subseteq B\wedge B\subseteq C)\to A\subseteq C$

Proof

1. Suppose $A\subseteq B\wedge B\subseteq C$.
2. $A\subseteq B$ [Specialisation on line 1]
3. $\forall a\in A[a\in B]$ [Definition of subset]
4. $B\subseteq C$ [Specialisation on line 1]
5. $\forall b\in B[b\in C]$ [Definition of subset]
6. Let $x\in A$ be arbitrarily chosen.
7. $x\in B$ [Universal instantiation on lines 3 and 6]
8. $x\in C$ [Universal instantiation on lines 5 and 7]
9. $\forall x\in A[x\in C]$ [Universal generalisation on lines 6 and 8]
10. $A\subseteq C$ [Definition of subset]
11. $(A\subseteq B\wedge B\subseteq C)\to A\subseteq C$ [Implication introduction on lines 1 and 10]

Example

$(A\subseteq C\wedge B\subseteq C)\to (A\cup B)\subseteq C$

Proof

1. Suppose $A\subseteq C\wedge B\subseteq C$.
2. $A\subseteq C$ [Specialisation on line 1]
3. $\forall x\in A[x\in C]$ [Definition of subset]
4. $B\subseteq C$ [Specialisation on line 1]
5. $\forall x\in B[x\in C]$ [Definition of subset]
6. Let $y\in A\cup B$ be arbitrarily chosen.
7. $y\in A\vee y\in B$ [Definition of set union]
8. Case 1: $y\in A$.
   1. Then $y\in C$. [Universal instantiation on lines 3 and 8]
9. Case 2: $y\in B$.
   1. Then $y\in C$. [Universal instantiation on lines 5 and 9]
10. In all cases, $y\in C$. [Proof by cases on lines 7, 8.1, 9.1]
11. $\forall y\in A\cup B[y\in C]$ [Universal generalisation on lines 6 and 10]
12. $A\cup B\subseteq C$ [Definition of subset]
13. $(A\subseteq C\wedge B\subseteq C)\to A\cup B\subseteq C$ [Implication introduction on lines 1 and 12]

Example

$A\cap B\subseteq A$

You can try this one for yourself; the answer has been hidden away in a spoiler tab.

Proof

1. Let $x\in A\cap B$ be arbitrarily chosen.
2. $x\in A\wedge x\in B$ [Definition of set intersection]
3. $x\in A$ [Specialisation on line 2]
4. $\forall x\in A\cup B[x\in A]$ [Universal generalisation on lines 1 and 3]
5. $A\cap B\subseteq A$ [Definition of subset]

Reasoning About Power Sets

Recall that $\mathcal{P}(A)$ is the set that contains all the subsets of $A$. This means that if we had to reason about subsets, that might mean we should use the concept of power sets.

Here are a few theorems that involve this concept:

1. $A\subseteq B\to \mathcal{P}(A)\subseteq \mathcal{P}(B)$
2. $\mathcal{P}(A\cap B)=\mathcal{P}(A)\cap \mathcal{P}(B)$

Example

$A\subseteq B\to \mathcal{P}(A)\subseteq \mathcal{P}(B)$

The proof of this uses the theorem that we proved in the previous section, namely:

$(A\subseteq B\wedge B\subseteq C)\to (A\subseteq C)$

Proof

1. Suppose $A\subseteq B$.
   1. Let $x\in \mathcal{P}(A)$ be arbitrarily chosen.
   2. $x\subseteq A$ [Definition of power set]
   3. $x\subseteq A\wedge A\subseteq B$ [Conjunction of lines 1 and 1.2]
   4. $x\subseteq B$ [Lemma]
   5. $x\in \mathcal{P}(B)$ [Definition of power set]
   6. $\forall x\in \mathcal{P}(A)[x\in \mathcal{P}(B)]$ [Universal generalisation on lines 1.1 and 1.5]
   7. $\mathcal{P}(A)\subseteq \mathcal{P}(B)$ [Definition of subset]
2. $A\subseteq B\to \mathcal{P}(A)\subseteq \mathcal{P}(B)$ [Implication introduction on lines 1 and 1.7]

Example

$\mathcal{P}(A\cap B)=\mathcal{P}(A)\cap \mathcal{P}(B)$

The proof for this has to work in two parts, we need to show two things:

1. $\mathcal{P}(A\cap B)\subseteq \mathcal{P}(A)\cap \mathcal{P}(B)$
2. $\mathcal{P}(A)\cap \mathcal{P}(B)\subseteq \mathcal{P}(A\cap B)$

Lines 1 through 1.15 will address part 1, and the remaining will address part 2. We’ll also use this lemma that will be left as an exercise for you to try to prove.

Lemma

$(X\subseteq A\wedge X\subseteq B)\to (X\subseteq A\cap B)$

Proof

1. Let $x\in \mathcal{P}(A\cap B)$ be arbitrarily chosen.
   1. Then $x\subseteq A\cap B$. [Definition of power set]
   2. $A\cap B\subseteq A$ [Lemma]
   3. $(x\subseteq A\cap B)\wedge (A\cap B\subseteq A)\to x\subseteq A$ [Lemma]
   4. $(x\subseteq A\cap B)\wedge (A\cap B\subseteq A)$ [Conjunction on lines 1.1 and 1.2]
   5. $x\subseteq A$ [Modus ponens on lines 1.3 and 1.4]
   6. $A\cap B\subseteq B$ [Lemma]
   7. $(x\subseteq A\cap B)\wedge (A\cap B\subseteq B)\to x\subseteq B$ [Lemma]
   8. $(x\subseteq A\cap B)\wedge (A\cap B\subseteq B)$ [Conjunction of lines 1.1 and 1.6]
   9. $x\subseteq B$ [Modus ponens on lines 1.7 and 1.8]
   10. $x\in \mathcal{P}(A)$ [Definition of power set from line 1.5]
   11. $x\in \mathcal{P}(B)$ [Definition of power set from line 1.9]
   12. $x\in \mathcal{P}(A)\wedge x\in \mathcal{P}(B)$ [Conjunction on lines 1.10 and 1.11]
   13. $x\in \mathcal{P}(A)\cap \mathcal{P}(B)$ [Definition of set intersection]
   14. $\forall x\in \mathcal{P}(A\cap B)[x\in \mathcal{P}(A)\cap \mathcal{P}(B)]$ [Universal generalisation on lines 1 and 1.13]
   15. $\mathcal{P}(A\cap B)\subseteq \mathcal{P}(A)\cap \mathcal{P}(B)$ [Definition of subset]
2. Let $y\in \mathcal{P}(A)\cap \mathcal{P}(B)$ be arbitrarily chosen.
   1. $y\in \mathcal{P}(A)\wedge y\in \mathcal{P}(B)$ [Definition of set intersection]
   2. $y\in \mathcal{P}(A)$ [Specialisation of line 2.1]
   3. $y\in \mathcal{P}(B)$ [Specialisation of line 2.1]
   4. $y\subseteq A$ [Definition of power set on line 2.2]
   5. $y\subseteq B$ [Definition of power set on line 2.3]
   6. $y\subseteq A\wedge y\subseteq B$ [Conjunction of lines 2.4 and 2.5]
   7. $(y\subseteq A\wedge y\subseteq B)\to (y\subseteq A\cap B)$ [Lemma]
   8. $y\subseteq A\cap B$ [Modus ponens on lines 2.6 and 2.7]
   9. $y\in \mathcal{P}(A\cap B)$ [Definition of power set]
   10. $\forall y\in \mathcal{P}(A)\cap \mathcal{P}(B)[y\in \mathcal{P}(A\cap B)]$ [Universal generalisation on lines 2 and 2.9]
   11. $\mathcal{P}(A)\cap \mathcal{P}(B)\subseteq \mathcal{P}(A\cap B)$ [Definition of subset]
3. $(\mathcal{P}(A\cap B)\subseteq \mathcal{P}(A)\cap \mathcal{P}(B))\wedge (\mathcal{P}(A)\cap \mathcal{P}(B)\subseteq \mathcal{P}(A\cap B))$ [Conjunction on lines 1.15 and 2.11]
4. $\mathcal{P}(A\cap B)=(\mathcal{P}(A)\cap \mathcal{P}(B))$ [Definition of set equivalence]

Bonus: Google Sheets

Let’s see some of the concepts in action. Let’s say that we are some marathon event organiser, and we had an initial Google Sheet that kept the data of the participants. For each participant, we keep track of their name, their gender, the marathon distance they have signed up for, and whether they have signed up as a beginner, or are in the open category.

So here’s an example of a sheet:

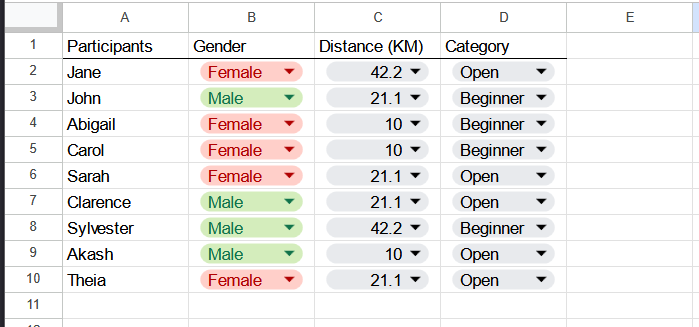
Let’s say we need to find out how which people are running 21.1 KM or more because they need to start earlier compared to the 10 KM runners. How should we do this? You’d use something like this formula:

=QUERY(Sheet1!A:D, "SELECT * WHERE C >= 21.1")

And if you did, you’d get this result on a new sheet:

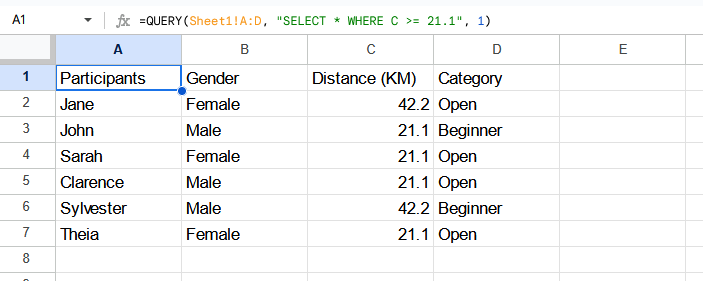
What is the QUERY syntax doing on the Google Sheet? It’s saying: “Go to Sheet1, look at columns A to D. Select any of the rows where the value in column C is at least 21.1.”

In some sense, you could probably see how this somewhat uses the concept of set-builder notation.

$$\{x\in \text{Sheet1}:x\text{’s distance is }\ge 21.1\}$$

Okay, what if after the competition, we tracked the participants that actually arrived and competed. We want to find out how many participants registered but did not show up on the day itself. How should we get this information? We probably want something like a set difference operation to help us out. Let $A$ be the set of registered participants and let $B$ be the set of participants we tracked that showed up. Then we can let $C=A\setminus B$ be the set we want to compute. And if you remember, we can write this in set-builder notation as:

$$C=\{x\in A:x\notin B\}$$

Google Sheets has something similar:

=FILTER(Sheet1!A:A, NOT(COUNTIF(Sheet2!A:A, Sheet1!A:A)))

This goes through all elements of Sheet1, and the FILTER formula basically means we are only allowing cells that satisfy the condition NOT(COUNTIF(Sheet2!A:A, Sheet1!A:A)) which is saying “not the case that the name in Sheet1 is also in Sheet2”.

Incidentally, databases like MySQL and PostgreSQL also have similar ideas on how to manipulate data. While we will not go into details in this module (since we do not cover databases), if you wish to have a sneak peek, you can take a look at their documentation here: MySQL, PostgreSQL.